题目内容
某物体质量为m,在光滑水平面上与运动方向相同的恒力F的作用下,发生一段位移L,速度由v1增加到v2.
(1)试从牛顿定律出发,导出动能定理的表达式.
(2)运用动能定理解答下面问题,有一质量m=2kg的物体,置于水平面上,在水平恒力F=8N的作用下,使物体由静止开始运动,经过x=4m后,撤去F,问物体还能运动多长距离?已知物体与水平面间动摩擦因数为μ=0.2.(g取10m/s2)
(1)试从牛顿定律出发,导出动能定理的表达式.
(2)运用动能定理解答下面问题,有一质量m=2kg的物体,置于水平面上,在水平恒力F=8N的作用下,使物体由静止开始运动,经过x=4m后,撤去F,问物体还能运动多长距离?已知物体与水平面间动摩擦因数为μ=0.2.(g取10m/s2)
分析:(1)根据牛顿第二定律和速度-位移关系公式列式后约去加速度即可得到动能定理表达式;
(2)对全过程运用动能定理求解物体还能运动多长距离.
(2)对全过程运用动能定理求解物体还能运动多长距离.
解答:解:(1)物体在恒力F作用下做匀加速运动,这个过程力F做的功为:W=FL
根据牛顿第二定律得:F=ma
而由运动学公式得:ν22-ν12=2aL
即:L=
把F、L的表达式代入W=FL得:W=
也就是:W=
mν22-
mν12,此式即为动能定理的表达式.
(2)对全过程,由动能定理:Fx-μmg(x+L)=0
得:L=
x=4m
答:(1)导出的动能定理的表达式是W=
mν22-
mν12.
(2)物体还能运动4m距离.
根据牛顿第二定律得:F=ma
而由运动学公式得:ν22-ν12=2aL
即:L=
| ν22-ν12 |
| 2a |
把F、L的表达式代入W=FL得:W=
| ma(ν22-ν12) |
| 2a |
也就是:W=
| 1 |
| 2 |
| 1 |
| 2 |
(2)对全过程,由动能定理:Fx-μmg(x+L)=0
得:L=
| (F-μmg) |
| μmg |
答:(1)导出的动能定理的表达式是W=
| 1 |
| 2 |
| 1 |
| 2 |
(2)物体还能运动4m距离.
点评:本题要掌握动能定理是由牛顿第二定律和速度-位移关系公式二合一推导出来的,应用动能定理时,要灵活选择研究过程,常有全程法和分段法两种选择方法.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
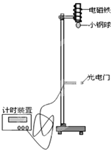 (Ⅰ)物体在空中下落的过程中,重力做正功,物体的动能越来越大,为了“探究重力做功和物体动能变化间的定量关系”,我们提供了如图的实验装置.
(Ⅰ)物体在空中下落的过程中,重力做正功,物体的动能越来越大,为了“探究重力做功和物体动能变化间的定量关系”,我们提供了如图的实验装置.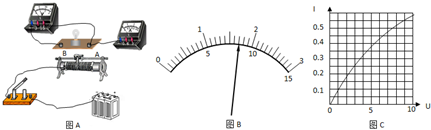
 (2010?卢湾区二模)图(a)是“DIS向心力实验器”,当质量为m的物体随旋转臂一起做半径为r的圆周运动时,受到的向心力可通过牵引杆由力传感器测得,旋转臂另一端的挡光杆每经过光电门一次,通过力传感器和光电门就同时获得一组向心力F和角速度ω的数据,并直接在坐标系中描出相应的点.得到多组F、ω的数据后,连成平滑的曲线,经验证为一个抛物线,改变实验条件重复三次实验(三次实验的条件见右表),得到的抛物线分别如图(b)中的①、②、③所示.
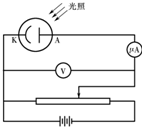
(2010?卢湾区二模)图(a)是“DIS向心力实验器”,当质量为m的物体随旋转臂一起做半径为r的圆周运动时,受到的向心力可通过牵引杆由力传感器测得,旋转臂另一端的挡光杆每经过光电门一次,通过力传感器和光电门就同时获得一组向心力F和角速度ω的数据,并直接在坐标系中描出相应的点.得到多组F、ω的数据后,连成平滑的曲线,经验证为一个抛物线,改变实验条件重复三次实验(三次实验的条件见右表),得到的抛物线分别如图(b)中的①、②、③所示. 物体在空中下落的过程中,重力做正功,物体的动能越来越大.为了“探究重力做功和物体动能变化间的定量关系”,某实验小组根据如图提供的实验装置设计的实验方案为:利用电磁铁控制小钢球的起始下落;用刻度尺测量小钢球的下落高度;用计时装置测出小钢球经过光电门的时间,计算出小钢球的速度;比较小钢球所受到的重力所做的功与小钢球动能变化之间的关系.
物体在空中下落的过程中,重力做正功,物体的动能越来越大.为了“探究重力做功和物体动能变化间的定量关系”,某实验小组根据如图提供的实验装置设计的实验方案为:利用电磁铁控制小钢球的起始下落;用刻度尺测量小钢球的下落高度;用计时装置测出小钢球经过光电门的时间,计算出小钢球的速度;比较小钢球所受到的重力所做的功与小钢球动能变化之间的关系.
 (3)快中子增殖反应堆中,使用的核燃料是钚239,裂变时释放出快中子,周围的铀238吸收快中子后变成铀239,铀239(92239U)很不稳定,经过
(3)快中子增殖反应堆中,使用的核燃料是钚239,裂变时释放出快中子,周围的铀238吸收快中子后变成铀239,铀239(92239U)很不稳定,经过 物体在空中下落的过程中,重力做正功,物体的动能越来越大,为了“探究重力做功和物体动能变化的定量关系”,我们提供了如右图的实验装置.
物体在空中下落的过程中,重力做正功,物体的动能越来越大,为了“探究重力做功和物体动能变化的定量关系”,我们提供了如右图的实验装置.