题目内容
 (2006?盐城一模)如图所示,间距为d的两平行板之间有方向向右的匀强电场,正方形容器abcd内有方向垂直纸面向里的匀强磁场,O为ab边的中点,ab边紧靠平行板.有两个质量均为m,电量均为q的带电粒子P1和P2在小孔处以初速度为零先后释放.P1经匀强电场加速后,从O处垂直正方形的ab边进入匀强磁场中,每一次和边碰撞时速度方向都垂直于被碰的边,当P1刚好回到O处时与后释放的P2相碰,以后P1、P2都在O处相碰.假设所有碰撞过程均无机械能损失.
(2006?盐城一模)如图所示,间距为d的两平行板之间有方向向右的匀强电场,正方形容器abcd内有方向垂直纸面向里的匀强磁场,O为ab边的中点,ab边紧靠平行板.有两个质量均为m,电量均为q的带电粒子P1和P2在小孔处以初速度为零先后释放.P1经匀强电场加速后,从O处垂直正方形的ab边进入匀强磁场中,每一次和边碰撞时速度方向都垂直于被碰的边,当P1刚好回到O处时与后释放的P2相碰,以后P1、P2都在O处相碰.假设所有碰撞过程均无机械能损失.(1)若在一个循环中P1和bc边只碰撞3次,求正方形的边长.
(2)若P1和P2在小孔O处刚碰撞后,立即改变平行板内电场强度和正方形容器内磁感应强度的大小,使P1不再与ab边碰撞,但仍和P2在O处碰撞.则电场强度和磁感应强度分别变为原来的几倍?
分析:(1)根据粒子在磁场中完成一个周期性运动的时间,及在电场中完成一个周期性运动的时间,即可求解;
(2)根据牛顿第二定律,由洛伦兹力提供向心力,得出半径与周期公式,再由动量定理,即可求解.
(2)根据牛顿第二定律,由洛伦兹力提供向心力,得出半径与周期公式,再由动量定理,即可求解.
解答:解:(1)由题意可知,ab边长L=6R
P1在磁场B中一个周期性运动的时间为t1=5T=5×
=
P2在电场E中一个周期性运动时间为t2=
=
由t1-t2得:L=
(2)由题意可知,ab边长L=R′=3R
R=
∝
∴B′=
P1在磁场B′中一个周期性运动的时间为
t3=T′=
=
=
t1
P2在电场E′中一个周期性运动的时间为
t4=
t2
P2电场中一个周期性运动的过程中由动量定理Ft=△P知:
qEt2=2mv
又qE′t4=2mv
∴E′=
E
答:(1)若在一个循环中P1和bc边只碰撞3次,则正方形的边长L=
.
(2)若P1和P2在小孔O处刚碰撞后,立即改变平行板内电场强度和正方形容器内磁感应强度的大小,使P1不再与ab边碰撞,但仍和P2在O处碰撞.则电场强度和磁感应强度分别变为原来的
倍.
P1在磁场B中一个周期性运动的时间为t1=5T=5×
| 2πR |
| v |
| 5πL |
| 3v |
P2在电场E中一个周期性运动时间为t2=
| 2d | ||
|
| 4d |
| v |
由t1-t2得:L=
| 12d |
| 5π |
(2)由题意可知,ab边长L=R′=3R
R=
| mv |
| qB |
| 1 |
| B |
∴B′=
| B |
| 3 |
P1在磁场B′中一个周期性运动的时间为
t3=T′=
| 2πR′ |
| v |
| 6πR |
| v |
| 3 |
| 5 |
P2在电场E′中一个周期性运动的时间为
t4=
| 3 |
| 5 |
P2电场中一个周期性运动的过程中由动量定理Ft=△P知:
qEt2=2mv
又qE′t4=2mv
∴E′=
| 5 |
| 3 |
答:(1)若在一个循环中P1和bc边只碰撞3次,则正方形的边长L=
| 12d |
| 5π |
(2)若P1和P2在小孔O处刚碰撞后,立即改变平行板内电场强度和正方形容器内磁感应强度的大小,使P1不再与ab边碰撞,但仍和P2在O处碰撞.则电场强度和磁感应强度分别变为原来的
| 5 |
| 3 |
点评:考查粒子在磁场与电场中运动的时间如何求解,掌握牛顿第二定律与动量定理,同时理解运动轨迹的半径与周期公式.

练习册系列答案
相关题目
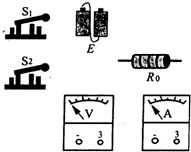 (2006?盐城一模)某同学准备测定一只量程已知的电压表的内阻,提供的器材及规格如下:
(2006?盐城一模)某同学准备测定一只量程已知的电压表的内阻,提供的器材及规格如下: