题目内容
 如图所示为粮袋的传送装霞.已知AB问长度为L.传送带与水平方向的夹角为θ.工作时运行速度为V,粮袋与传送带间的动摩擦因数为?,正常工作时工人在A端将粮袋放到运行中的传送带上,关于粮袋从A到B的运动,以下说法正确的是(设最大静摩擦力等于滑动摩擦力)( )
如图所示为粮袋的传送装霞.已知AB问长度为L.传送带与水平方向的夹角为θ.工作时运行速度为V,粮袋与传送带间的动摩擦因数为?,正常工作时工人在A端将粮袋放到运行中的传送带上,关于粮袋从A到B的运动,以下说法正确的是(设最大静摩擦力等于滑动摩擦力)( )分析:解答本题要通过分析粮袋的受力情况,来确定其运动情况:
若μ≥tanθ,粮袋可能一直受到滑动摩擦力作用,一直是做匀加速运动,也可能先受到滑动摩擦力后受到静摩擦力而做匀速运动.
开始时,粮袋受到沿传送带向下的滑动摩擦力,根据牛顿第二定律可求得加速度;若L足够大,若?<tanθ,粮袋不可能做匀速运动;
根据μ与tanθ的大小关系,粮袋在传送带上可能一直做匀加速运动;可能先匀加速运动,当速度与传送带相同后,做匀速运动,到达B点时速度与v相同;也可能先做加速度较大的匀加速运动,分析粮袋到达B端的速度与v大小.
若μ≥tanθ,粮袋可能一直受到滑动摩擦力作用,一直是做匀加速运动,也可能先受到滑动摩擦力后受到静摩擦力而做匀速运动.
开始时,粮袋受到沿传送带向下的滑动摩擦力,根据牛顿第二定律可求得加速度;若L足够大,若?<tanθ,粮袋不可能做匀速运动;
根据μ与tanθ的大小关系,粮袋在传送带上可能一直做匀加速运动;可能先匀加速运动,当速度与传送带相同后,做匀速运动,到达B点时速度与v相同;也可能先做加速度较大的匀加速运动,分析粮袋到达B端的速度与v大小.
解答:解:A、若μ≥tanθ,粮袋可能一直受到滑动摩擦力作用,一直是做匀加速运动;也可能先匀加速运动,当速度与传送带相同后,做匀速运动.故A错误.
B、粮袋开始运动时受到沿传送带向下的滑动摩擦力,根据牛顿第二定律得:加速度为a=
=g(sinθ+?cosθ).故B错误.
C、由上分析可知,粮袋从A到B不一定一直匀加速运动.若?<tanθ,粮袋的速度与传送带相同后,加速度为g(sinθ-?cosθ)<gsinθ.故C错误.
D、粮袋在传送带上可能一直做匀加速运动,到达B点时的速度小于v;可能先匀加速运动,当速度与传送带相同后,做匀速运动,到达B点时速度与v相同;也可能先做加速度较大的匀加速运动,当速度与传送带相同后做加速度较小的匀加速运动,到达B点时的速度大于v;故D正确.
故选D
B、粮袋开始运动时受到沿传送带向下的滑动摩擦力,根据牛顿第二定律得:加速度为a=
| mgsinθ+μmgcosθ |
| m |
C、由上分析可知,粮袋从A到B不一定一直匀加速运动.若?<tanθ,粮袋的速度与传送带相同后,加速度为g(sinθ-?cosθ)<gsinθ.故C错误.
D、粮袋在传送带上可能一直做匀加速运动,到达B点时的速度小于v;可能先匀加速运动,当速度与传送带相同后,做匀速运动,到达B点时速度与v相同;也可能先做加速度较大的匀加速运动,当速度与传送带相同后做加速度较小的匀加速运动,到达B点时的速度大于v;故D正确.
故选D
点评:本题考查分析物体运动情况的能力,而要分析物体的运动情况,首先要具有物体受力情况的能力.传送带问题,物体的运动情况比较复杂,关键要考虑物体的速度能否与传送带相同.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 (2012?湖北模拟)如图所示为粮袋的传送装置,已知AB间长度为L,传送带与水平方向的夹角为θ,工作时运行速度为v,粮袋与传送带间的动摩擦因数为μ,正常工作时工人在A点将粮袋放到运行中的传送带上,关于粮袋从A到B的运动,以下说法正确的是(设最大静摩擦力等于滑动摩擦力)( )
(2012?湖北模拟)如图所示为粮袋的传送装置,已知AB间长度为L,传送带与水平方向的夹角为θ,工作时运行速度为v,粮袋与传送带间的动摩擦因数为μ,正常工作时工人在A点将粮袋放到运行中的传送带上,关于粮袋从A到B的运动,以下说法正确的是(设最大静摩擦力等于滑动摩擦力)( ) ,工作时逆时针运行速度为v,粮袋与传送带间的动摩擦因数为
,工作时逆时针运行速度为v,粮袋与传送带间的动摩擦因数为 ,正常工作时工人在A点将粮袋轻放到运行中的传送带上,关于粮袋从A到B的运动,以下说法正确的是(设最大静摩擦力等于滑动摩擦力)(
)
,正常工作时工人在A点将粮袋轻放到运行中的传送带上,关于粮袋从A到B的运动,以下说法正确的是(设最大静摩擦力等于滑动摩擦力)(
)
 足够大,粮袋轻放在A时可能立刻与传送带一起匀速运动
足够大,粮袋轻放在A时可能立刻与传送带一起匀速运动 ,
从A到B的时间可能等于
,
从A到B的时间可能等于 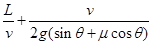
 和L值多大,粮袋的速度不可能超过
和L值多大,粮袋的速度不可能超过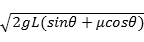

 ,工作时运行速度为
,工作时运行速度为 ,粮袋与传送带间的动摩擦因数为
,粮袋与传送带间的动摩擦因数为 ,正常工作时工人在A点将粮袋放到运行中的传送带上,关于粮袋从A到B的运动,以下说法正确的是(设最大静摩擦力等于滑动摩擦力) ( )
,正常工作时工人在A点将粮袋放到运行中的传送带上,关于粮袋从A到B的运动,以下说法正确的是(设最大静摩擦力等于滑动摩擦力) ( )
 ,若L足够大,则以后将一定以速度
,若L足够大,则以后将一定以速度 做匀速运动
做匀速运动
 ,则粮袋从A到B一定一直是做加速运动
,则粮袋从A到B一定一直是做加速运动
