题目内容
6. 在如图所示的电路中,电源的电动势E=9.0V,内阻r=1.0Ω.电阻R1=10Ω,R2=10Ω,R3=30Ω,R4=35Ω;电容器的电容C=100 μF.电容器原来不带电.求:
在如图所示的电路中,电源的电动势E=9.0V,内阻r=1.0Ω.电阻R1=10Ω,R2=10Ω,R3=30Ω,R4=35Ω;电容器的电容C=100 μF.电容器原来不带电.求:(1)电源的输出功率.
(2)一分钟内R1上产生的热量.
(3)接通电键K后流过R4的总电荷量.
分析 (1)先求出外电路总电阻,再由闭合电路欧姆定律求出总电流,即可求解电源的输出功率.
(2)求出路端电压,再由焦耳定律求R1上产生的热量.
(3)接通开关S待电路稳定后电容器两板间的电压等于电阻R3两端的电压.根据欧姆定律和串并电路的特点,求出电压UC;接通开关S到电路稳定过程中流过R4的总电荷量Q等于电容器所带的电量,根据电容的定义式求解Q.
解答 解:(1)外电路总电阻为:R=$\frac{{R}_{1}({R}_{2}+{R}_{3})}{{R}_{1}+{R}_{2}+{R}_{3}}$=$\frac{10×(10+30)}{10+10+30}$Ω=8Ω
总电流为:I=$\frac{E}{R+r}$=$\frac{9}{8+1}$A=1A
故电源的输出功率为:P=EI-I2r=9×1-12×1=8W.
(2)路端电压为:U=E-Ir=9-1×1=8V
一分钟内R1上产生的热量为:Q=$\frac{{U}^{2}}{{R}_{1}}$t=$\frac{{8}^{2}}{10}×60$J=288J.
(3)电容器两板间电压等于R3两端电压为:
UC=U3=$\frac{{R}_{3}}{{R}_{2}+{R}_{3}}$U=$\frac{30}{40}$×8V=6V
流过R4的电荷量为:Q=CUC
得:Q=6×10-4C
答:(1)电源的输出功率是8W.
(2)一分钟内R1上产生的热量是288J.
(3)接通电键K后流过R4的总电荷量是6×10-4C.
点评 对于含有电容器的问题,关键是确定电容器的电压.电路稳定时电容器的电压等于其并联电路两端的电压.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
17.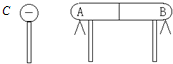 取一对用绝缘支柱支持的金属导体A、B,使它们彼此接触,如图所示.起初它们不带电,现将一带负电的球C移近导体A,发现A、B上的金属箔都张开了,则( )
取一对用绝缘支柱支持的金属导体A、B,使它们彼此接触,如图所示.起初它们不带电,现将一带负电的球C移近导体A,发现A、B上的金属箔都张开了,则( )
 取一对用绝缘支柱支持的金属导体A、B,使它们彼此接触,如图所示.起初它们不带电,现将一带负电的球C移近导体A,发现A、B上的金属箔都张开了,则( )
取一对用绝缘支柱支持的金属导体A、B,使它们彼此接触,如图所示.起初它们不带电,现将一带负电的球C移近导体A,发现A、B上的金属箔都张开了,则( )| A. | 此时A带正电,B带正电 | |
| B. | 此时A带负电,B带正电 | |
| C. | 此时若先将A、B分开,再移去C,则A带正电,B带负电 | |
| D. | 此时若先移去C,再将A、B分开,则A带正电,B带负电 |
14.对于一定质量的理想气体,以下情况不可能出现的是( )
| A. | 温度不变,压强增加,放出热量 | B. | 温度增加,体积减小,吸收热量 | ||
| C. | 体积增加,压强减小,吸收热量 | D. | 温度不变,对外做功,放出热量 |
 质量为m=1kg的滑块以水平初速度v0=4m/s滑上静止在光滑水平面上的质量M=3kg的长木板,最后二者以共同速度运动,滑块与木板间的动摩擦因数为0.2,求:
质量为m=1kg的滑块以水平初速度v0=4m/s滑上静止在光滑水平面上的质量M=3kg的长木板,最后二者以共同速度运动,滑块与木板间的动摩擦因数为0.2,求: 如图所示,倾斜轨道AB的倾角为37°,CD、EF轨道水平,AB与CD通过光滑圆弧管道BC连接,CD右端与竖直光滑圆周轨道相连.小球可以从D进入该轨道,沿轨道内侧运动,从E滑出该轨道进入EF水平轨道.小球由静止从A点释放,已知AB长为5R,CD长为R,重力加速度为g,小球与斜轨AB及水平轨道CD、EF的动摩擦因数均为0.5,sin37°=0.6,cos37°=0.8,圆弧管道BC入口B与出口C的高度差为l.8R.求:(在运算中,根号中的数值无需算出)
如图所示,倾斜轨道AB的倾角为37°,CD、EF轨道水平,AB与CD通过光滑圆弧管道BC连接,CD右端与竖直光滑圆周轨道相连.小球可以从D进入该轨道,沿轨道内侧运动,从E滑出该轨道进入EF水平轨道.小球由静止从A点释放,已知AB长为5R,CD长为R,重力加速度为g,小球与斜轨AB及水平轨道CD、EF的动摩擦因数均为0.5,sin37°=0.6,cos37°=0.8,圆弧管道BC入口B与出口C的高度差为l.8R.求:(在运算中,根号中的数值无需算出)