题目内容
 一个处于基态的氢原子射向另一个处于基态的静止的氢原子发生碰撞并连成一体,损失的动能使其中的一个氢原子跃迁到激发态,这个氢原子最多能发出两个不同频率的光子.已知:元电荷e=1.6×10-19C,真空中光速c=3.0×108m/s,普朗克常量h=6.63×10-34Js,光子的动量可以不计,氢原子能级如图所示.求:
一个处于基态的氢原子射向另一个处于基态的静止的氢原子发生碰撞并连成一体,损失的动能使其中的一个氢原子跃迁到激发态,这个氢原子最多能发出两个不同频率的光子.已知:元电荷e=1.6×10-19C,真空中光速c=3.0×108m/s,普朗克常量h=6.63×10-34Js,光子的动量可以不计,氢原子能级如图所示.求:(1)碰撞后跃迁到激发态的氢原子所处能级的量子数n及该氢原子碰撞前后的能量值
(2)两个不同频率的光子中波长较短的光子的波长值.
(3)入射氢原子的动能.
分析:(1)处于量子数为n激发态的氢原子能发出C
种频率不同的光子;对照能级图可得到该氢原子碰撞前后的能量值.
(2)根据玻尔理论:Em-En=hγ=h
(m>n),两个能级差越大,所放出的光子波长越长.
(3)两个氢原子发生完全非弹性碰撞,根据动量守恒定律和能量守恒定律求入射氢原子的动能.
2 n |
(2)根据玻尔理论:Em-En=hγ=h
| c |
| λ |
(3)两个氢原子发生完全非弹性碰撞,根据动量守恒定律和能量守恒定律求入射氢原子的动能.
解答:解:(1)处于量子数为n激发态的氢原子能发出C
种频率不同的光子,因为碰撞后的氢原子最多能发出两个不同频率的光子,所以碰撞使氢原子从基态跃迁到n=3的激发态.
由氢原子能级图可知,氢原子在这两个状态的能量分别为:
E1=-13.60eV,E3=-1.51eV
(2)波长较短的光子是氢原子是从n=2的激发态跃迁到基态发出的,由氢原子能级图可知,氢原子在n=2的激发态的能量为E2=-3.40eV,由玻尔理论得:
E2-E1=
得波长较短的光子的波长值为
λ=
=
m=1.22×10-7m
(3)设氢原子质量为m,入射氢原子的入射速度为v0,两个氢原子发生完全非弹性碰撞后的速度为v,根据动量守恒定律和能量守恒定律有
mv0=2mv
E3-E1=
mv02-
(2m)v2
所以,入射氢原子的动能为
Ek0=
mv02=2(E3-E1)=24.18eV
答:
(1)碰撞后跃迁到激发态的氢原子所处能级的量子数n为3个,该氢原子碰撞前后的能量值分别为,-13.60eV,-1.51eV.
(2)两个不同频率的光子中波长较短的光子的波长值为1.22×10-7m.
(3)入射氢原子的动能为24.18eV.
2 n |
由氢原子能级图可知,氢原子在这两个状态的能量分别为:
E1=-13.60eV,E3=-1.51eV
(2)波长较短的光子是氢原子是从n=2的激发态跃迁到基态发出的,由氢原子能级图可知,氢原子在n=2的激发态的能量为E2=-3.40eV,由玻尔理论得:
E2-E1=
| hc |
| λ |
得波长较短的光子的波长值为
λ=
| hc |
| E2-E1 |
| 6.63×10-34×3.0×108 |
| [(-3.40)-(-13.60)]×1.60×10-19 |
(3)设氢原子质量为m,入射氢原子的入射速度为v0,两个氢原子发生完全非弹性碰撞后的速度为v,根据动量守恒定律和能量守恒定律有
mv0=2mv
E3-E1=
| 1 |
| 2 |
| 1 |
| 2 |
所以,入射氢原子的动能为
Ek0=
| 1 |
| 2 |
答:
(1)碰撞后跃迁到激发态的氢原子所处能级的量子数n为3个,该氢原子碰撞前后的能量值分别为,-13.60eV,-1.51eV.
(2)两个不同频率的光子中波长较短的光子的波长值为1.22×10-7m.
(3)入射氢原子的动能为24.18eV.
点评:本题要掌握玻尔理论,知道氢原子从高能级往低能级跃迁时是随机的,可发出C
种频率不同的光子;两个氢原子发生完全非弹性碰撞同样遵守动量守恒定律和能量守恒定律.
2 n |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
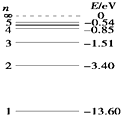 氢原子能级如图所示,则要使一个处于基态的氢原子释放出一个电子而变成为氢离子,该氢原子需要吸收的能量至少是
氢原子能级如图所示,则要使一个处于基态的氢原子释放出一个电子而变成为氢离子,该氢原子需要吸收的能量至少是
