Question

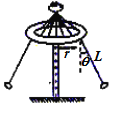
【题目】“旋转秋千”是游乐园里常见的游乐项目，其基本装置是将绳子上端固定在转盘的边上，绳子下端连接座椅，人坐在座椅上随转盘旋转而在空中飞旋。若将人和座椅看为质点，“旋转秋千”可简化为如图所示的模型。其中，处于水平面内的圆形转盘，半径为r，可绕穿过其中心的竖直轴转动。让转盘由静止开始逐渐加速转动，经过一段时间后质点与转盘一起以角速度做匀速圆周运动，此时绳子与竖直方向的夹角为θ。已知绳长为L且不可伸长，质点的质量为m，不计空气阻力及绳重。则下列说法中正确的是（ ）

A. 质点的重力越大，绳子与竖直方向的夹角θ越小

B. 质点做匀速圆周运动的向心力是其所受悬线的拉力

C. 转盘转动的角速度与夹角θ的关系为

D. 质点从静止到做匀速圆周运动的过程中，绳子对质点做的功为

Answer 1

【答案】C

【解析】

由重力和绳子的拉力的合力提供质点圆周运动的向心力，如图，则有：mgtanθ=mω2R
解得：tanθ=，与重力无关，故A、B错误；

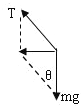
质点做匀速圆周运动的向心力是由重力和绳子的拉力的合力提供的，故B错误；根据mgtanθ=mω2R=mω2（r+Lsinθ）解得：，故C正确；设质点与转盘一起做匀速圆周运动时速度大小为v，根据向心力公式得：mgtanθ=m…①
对于质点从静止到做匀速圆周运动的过程中，重力做功为-mgl（1-cosθ），设绳子拉力做功为W，则根据动能定理得：W-mgl（1-cosθ）=mv2…②
联立①②得：W=mgl（1-cosθ）+mg（r+Lsinθ）tanθ，故D错误。故选C。