题目内容
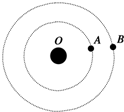如图所示，有A、B两颗行星绕同一恒星O做圆周运动，运转方向相同，A行星的周期为T1，B行星的周期为T2，在某一时刻两行星第一次相遇（即相距最近），则（ ）| A、经过时间t=T1+T2两行星将第二次相遇 | ||
B、经过时间t=
| ||
C、经过时间t=
| ||
D、经过时间t=
|
分析：人造卫星在不同的轨道上运动，先求出角速度，再一次追上B多转动一圈，多转动半圈时相距最远．
解答：解：A、B、多转动一圈时，第二次追上，有：
t-
t=2π
解得：t=
故A错误，B正确；
C、D、多转动半圈时，第一次相距最远，有：
t′-
t′=π
解得：t′=
故C错误，D正确；
故选：BD．
| 2π |
| T1 |
| 2π |
| T2 |
解得：t=
| T1T2 |
| T2-T1 |
故A错误，B正确；
C、D、多转动半圈时，第一次相距最远，有：
| 2π |
| T1 |
| 2π |
| T2 |
解得：t′=
| T1T2 |
| 2(T2-T1) |
故C错误，D正确；
故选：BD．
点评：本题是有关转动的追击问题，每次多转动一圈后追上一次，多转动（n+
）圈相距最远．
| 1 |
| 2 |
练习册系列答案
相关题目
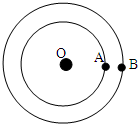如图所示，有A、B两个行星绕同一恒星O沿不同轨道做匀速圆周运动，旋转方向相同．A行星的周期为T1，B行星的周期为T2，在某一时刻两行星第一次相遇（即两行星距离最近），则（ ）
