题目内容
 倾斜雪道的长为25m,顶端高为15m,下端经过一小段圆弧过渡后与很长的水平雪道相接,如图所示.一滑雪运动员在倾斜雪道的顶端以水平速度v0=8m/s飞出,在落到倾斜雪道上时,运动员靠改变姿势进行缓冲使自己只保留沿斜面的分速度而不弹起.除缓冲外运动员可视为质点,过渡轨道光滑,其长度可忽略.设滑雪板与雪道的动摩擦因数μ=0.2,求运动员在水平雪道上滑行的距离(取g=10m/s2)
倾斜雪道的长为25m,顶端高为15m,下端经过一小段圆弧过渡后与很长的水平雪道相接,如图所示.一滑雪运动员在倾斜雪道的顶端以水平速度v0=8m/s飞出,在落到倾斜雪道上时,运动员靠改变姿势进行缓冲使自己只保留沿斜面的分速度而不弹起.除缓冲外运动员可视为质点,过渡轨道光滑,其长度可忽略.设滑雪板与雪道的动摩擦因数μ=0.2,求运动员在水平雪道上滑行的距离(取g=10m/s2)分析:根据平抛运动的规律求出平抛运动的时间,求出水平位移和竖直位移,从而确定落点与抛出点的距离,分别求出水平方向和竖直方向上的分速度,知垂直于斜面方向上的分速度为零,最终的速度沿斜面方向,根据动能定理求出运动员在水平雪道上滑行的距离.
解答: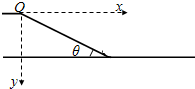 解:如图选坐标,斜面的方程为:y=xtanθ=
解:如图选坐标,斜面的方程为:y=xtanθ=
x ①
运动员飞出后做平抛运动x=v0t ②
y=
gt2 ③
联立①②③式,得飞行时间
t=1.2 s
落点的x坐标:x1=v0t=9.6 m
落点离斜面顶端的距离:s1=
=12m
落点距地面的高度:h1=(L-s1)sinθ=7.8m
接触斜面前的x分速度:vx=8m/s
y分速度:vy=gt=12m/s
沿斜面的速度大小为:vB=vxcosθ+vysinθ=13.6m/s
设运动员在水平雪道上运动的距离为s2,由功能关系得:mgh+
m
=μmgcosθ(L-s1)+μmgs2
解得:s2=74.8 m
答:运动员在水平雪道上滑行的距离为74.8m.
 解:如图选坐标,斜面的方程为:y=xtanθ=
解:如图选坐标,斜面的方程为:y=xtanθ=| 3 |
| 4 |
运动员飞出后做平抛运动x=v0t ②
y=
| 1 |
| 2 |
联立①②③式,得飞行时间
t=1.2 s
落点的x坐标:x1=v0t=9.6 m
落点离斜面顶端的距离:s1=
| x |
| cosθ |
落点距地面的高度:h1=(L-s1)sinθ=7.8m
接触斜面前的x分速度:vx=8m/s
y分速度:vy=gt=12m/s
沿斜面的速度大小为:vB=vxcosθ+vysinθ=13.6m/s
设运动员在水平雪道上运动的距离为s2,由功能关系得:mgh+
| 1 |
| 2 |
| v | 2 B |
解得:s2=74.8 m
答:运动员在水平雪道上滑行的距离为74.8m.
点评:解决本题的关键通过平抛运动的规律求出落在斜面上沿斜面方向的速度,通过动能定理进行求解.

练习册系列答案
相关题目
 倾斜雪道的长为25m,顶端高为15m,下端经过一小圆弧过渡后与很长的水平雪道相接,如图所示.一滑雪运动员在倾斜雪道的顶端以水平速度v0=8m/s飞出.在落到倾斜雪道上时,运动员靠改变姿势进行缓冲使自己只保留沿斜面的分速度面不弹起.除缓冲过程外运动员可视为质点,过渡圆弧光滑,其长度可忽略.设滑雪板与雪道的动摩擦因数μ=0.2,取g=10m/s2.
倾斜雪道的长为25m,顶端高为15m,下端经过一小圆弧过渡后与很长的水平雪道相接,如图所示.一滑雪运动员在倾斜雪道的顶端以水平速度v0=8m/s飞出.在落到倾斜雪道上时,运动员靠改变姿势进行缓冲使自己只保留沿斜面的分速度面不弹起.除缓冲过程外运动员可视为质点,过渡圆弧光滑,其长度可忽略.设滑雪板与雪道的动摩擦因数μ=0.2,取g=10m/s2. 倾斜雪道的长为25m,顶端高为15m,下端经过一小段圆弧过渡后与很长的水平雪道相接,如图所示.一滑雪运动员在倾斜雪道的顶端以水平速度v0=8m/s飞出,在落到倾斜雪道上时,运动员靠改变姿势进行缓冲使自己只保留沿斜面的分速度而不弹起.除缓冲外运动员可视为质点,过渡轨道光滑,其长度可忽略.设滑雪板与雪道的动摩擦因数μ=0.2,求:(g取10m/s2)
倾斜雪道的长为25m,顶端高为15m,下端经过一小段圆弧过渡后与很长的水平雪道相接,如图所示.一滑雪运动员在倾斜雪道的顶端以水平速度v0=8m/s飞出,在落到倾斜雪道上时,运动员靠改变姿势进行缓冲使自己只保留沿斜面的分速度而不弹起.除缓冲外运动员可视为质点,过渡轨道光滑,其长度可忽略.设滑雪板与雪道的动摩擦因数μ=0.2,求:(g取10m/s2)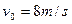 飞出。在落到倾斜雪道上时,运动员靠改变姿势进行缓冲使自己只保留沿斜面的分速度面不弹起。除缓冲过程外运动员可视为质点,过渡圆弧光滑,其长度可忽略。设滑雪板与雪道的动摩擦因数
飞出。在落到倾斜雪道上时,运动员靠改变姿势进行缓冲使自己只保留沿斜面的分速度面不弹起。除缓冲过程外运动员可视为质点,过渡圆弧光滑,其长度可忽略。设滑雪板与雪道的动摩擦因数 ,取
,取 。
。