题目内容
 (2007?广州一模)质量分别为3m和m的两个物体,用一根细线相连,中间夹着一个被压缩的轻质弹簧,整个系统原来在光滑水平地面上以速度υ0向右匀速运动,如图所示.后来细线断裂,质量为m的物体离开弹簧时的速度变为2υ0.
(2007?广州一模)质量分别为3m和m的两个物体,用一根细线相连,中间夹着一个被压缩的轻质弹簧,整个系统原来在光滑水平地面上以速度υ0向右匀速运动,如图所示.后来细线断裂,质量为m的物体离开弹簧时的速度变为2υ0.求:弹簧在这个过程中做的总功.
分析:细线断裂过程,系统的合外力为零,总动量守恒,根据动量守恒定律就可以求出物体m离开弹簧时物体3m的速度,根据动能定理分别求出弹簧对两个物体做的功,两者之和即可得到弹簧在这个过程中做的总功.
解答:解:设3m的物体离开弹簧时的速度为υ',根据动量守恒定律,
则有:(3m+m)υ0=m?2υ0+3mυ'
解得:υ′=
υ0
根据动能定理,弹簧对两个物体做的功分别为:
W1=
m(2υ0)2-
m
=
m
W2=
?3m?(
)2-
?3m?
=-
m
所以弹簧做的总功:W=W1+W2=
m
答:弹簧在这个过程中做的总功为
m
.
则有:(3m+m)υ0=m?2υ0+3mυ'
解得:υ′=
| 2 |
| 3 |
根据动能定理,弹簧对两个物体做的功分别为:
W1=
| 1 |
| 2 |
| 1 |
| 2 |
| υ | 2 0 |
| 3 |
| 2 |
| υ | 2 0 |
W2=
| 1 |
| 2 |
| 2 |
| 3 |
| υ | 0 |
| 1 |
| 2 |
| υ | 2 0 |
| 5 |
| 6 |
| υ | 2 0 |
所以弹簧做的总功:W=W1+W2=
| 2 |
| 3 |
| υ | 2 0 |
答:弹簧在这个过程中做的总功为
| 2 |
| 3 |
| v | 2 0 |
点评:本题是系统动量守恒和机械能守恒的类型,对于弹簧的弹力是变力,应运用动能定理求解做功.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
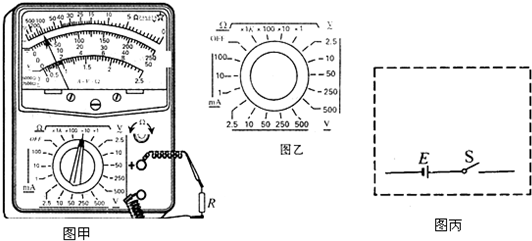
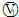 内阻
内阻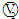 ,量程3V,内阻约15kΩ左右)
,量程3V,内阻约15kΩ左右) (2007?广州一模)两根相距为L的足够长的平行金属直角导轨MNP与M′N′P′如图所示那样放置,MN与M′N′在同一水平面内、NP与N′P′沿竖直方向.水平金属细杆ab、cd分别与导轨垂直接触形成闭合回路,cd杆质量为m、与导轨之间的动摩擦因数为μ,导轨电阻不计,回路总电阻为R.整个装置处于磁感应强度大小为B、方向竖直向下的匀强磁场中.当ab杆在平行于水平导轨的拉力作用下以某一速度沿导轨匀速向左运动时,cd杆恰好竖直向下匀速运动.重力加速度为g.求:
(2007?广州一模)两根相距为L的足够长的平行金属直角导轨MNP与M′N′P′如图所示那样放置,MN与M′N′在同一水平面内、NP与N′P′沿竖直方向.水平金属细杆ab、cd分别与导轨垂直接触形成闭合回路,cd杆质量为m、与导轨之间的动摩擦因数为μ,导轨电阻不计,回路总电阻为R.整个装置处于磁感应强度大小为B、方向竖直向下的匀强磁场中.当ab杆在平行于水平导轨的拉力作用下以某一速度沿导轨匀速向左运动时,cd杆恰好竖直向下匀速运动.重力加速度为g.求: (2007?广州一模)如图所示,在水平地面正上方有范围足够大的匀强磁场和匀强电场(图中未画出电场线).已知磁场的磁感应强度为B,方向水平并垂直纸面向里.一质量为m、带电量为-q的带电微粒在此区域恰好作速度为υ的匀速圆周运动.(重力加速度为g,空气阻力可忽略).
(2007?广州一模)如图所示,在水平地面正上方有范围足够大的匀强磁场和匀强电场(图中未画出电场线).已知磁场的磁感应强度为B,方向水平并垂直纸面向里.一质量为m、带电量为-q的带电微粒在此区域恰好作速度为υ的匀速圆周运动.(重力加速度为g,空气阻力可忽略). (2007?广州一模)如图所示,在光滑水平地面上静放着质量mA=2kg的滑块A(可看成质点)和质量mB=4kg、长L=6m的薄板B.设A、B间动摩擦因数为μ=0.2,且A、B之间的最大静摩擦力与滑动摩擦力大小相等.因向B板施加水平拉力F=20N,F作用2s后撤去F,取g=10m/s2.求:
(2007?广州一模)如图所示,在光滑水平地面上静放着质量mA=2kg的滑块A(可看成质点)和质量mB=4kg、长L=6m的薄板B.设A、B间动摩擦因数为μ=0.2,且A、B之间的最大静摩擦力与滑动摩擦力大小相等.因向B板施加水平拉力F=20N,F作用2s后撤去F,取g=10m/s2.求: