题目内容
11.如图所示,AB段是光滑斜面,水平段BC使用长度可调的水平传送带,BC长计为L,传送带顺时针转动的速率v0=2m/s,设质量为m=0.1kg的小物块由静止开始从距水平传送带高为h处下滑,经过B点的拐角处无机械能损失,物块与传送带间的滑动摩擦因数μ=0.4.小物块随传送带运动到C点后水平抛出,恰好无碰撞的沿着圆弧切线从D点进入竖直面内的光滑圆弧轨道DMN,并沿轨道恰好通过最高点N,O为圆弧的圆心,MN为其竖直直径,OD与竖直方向的夹角为60°,圆弧半径R=0.9m.试求:(1)小物块经过M点时对圆弧轨道的压力的大小;
(2)小物块离开C点时的速度大小;
(3)高度h与BC长度L满足的关系;
(4)若h=1.25m,则运动过程中产生的热量Q为多少?
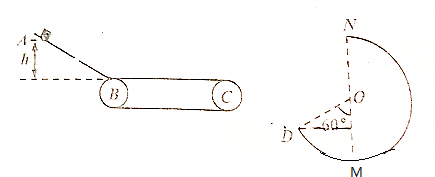
分析 (1)小物块沿轨道恰好通过最高点N,可得在N点时的速度大小,应用动能定理可得在M点时的速度大小,由牛顿第二定律求得经过M点时圆弧轨道的支持力的大小,从而由牛顿第三定律得到对圆弧轨道的压力的大小.
(2)从D到M点应用动能定理可得在D点时的速度大小,由于恰好无碰撞的沿着圆弧切线从D点进入竖直面内的光滑圆弧轨道DMN,对D点的速度进行分解,有几何关系可得水平方向的分速度,就是从C点抛出时的速度.
(3)结合(2)的结果,对于物块从A到C得运动应用动能定理或牛顿运动定律求解即可.
(4)若h=1.25m,结合(2)的结果可得则运动过程中摩擦力的负功,该负功将产生产生的热量Q.
解答 解:(1)小物块沿轨道恰好通过最高点N,可得在N点时的速度大小v1满足:mg=$\frac{{mv}_{1}^{2}}{R}$ ①
物体从M到N应用动能定理可得,-mg•2R=$\frac{1}{2}$${mv}_{1}^{2}-\frac{1}{2}$${mv}_{M}^{2}$ ②
在M点,轨道的支持力为FN,由牛顿第二定律可得:${F}_{N}-mg=\frac{{mv}_{M}^{2}}{R}$ ③
由牛顿第三定律可得,小物块经过M点时对圆弧轨道的压力F=FN ④
解①②③④得,F=6mg=6×0.1×10N=6N
(2)从N到D应用动能定理可得,mgR(1+cos60°)=$\frac{1}{2}$${mv}_{D}^{2}-\frac{1}{2}$${mv}_{N}^{2}$ ⑤
由于恰好无碰撞的沿着圆弧切线从D点进入竖直面内的光滑圆弧轨道DMN,故有水平方向的分速度为vx=vDcos60° ⑥
而vC=vx ⑦
由①⑤⑥⑦得,vC=$\frac{\sqrt{2gR}}{2}$=2.12m/s
(3)由于vC>v0,物块在传送带上始终做匀减速运动,对于物块从下滑开始到抛出的过程有动能定理可得:
mgh-$μmgL=\frac{1}{2}$${mv}_{C}^{2}$ ⑧
带入数据得高度h与BC长度L满足的关系:5h-2L=2.2 ⑨
(4)若h=1.25m,则运动过程中产生的热量Q=μmgL(10)
联立⑨(10)并代入数据得,Q≈0.8J
答:(1)小物块经过M点时对圆弧轨道的压力为6N;
(2)小物块离开C点时的速度大小为2.12m/s;
(3)高度h与BC长度L满足的关系为5h-2L=2.2;
(4)若h=1.25m,则运动过程中产生的热量Q为0.8J.
点评 此题是一道非常好的题,考察到了多个知识点.
首先是考察到了机械能守恒定律,我们要了解机械能守恒定律的条件和表达式,在机械能的表达式上要注意灵活,可从守恒的角度写成E1=E2或△E=0,可从能量转化的角度写成△Ek增=△Ep减,从两物体间能的转移角度写成△EA增=△EB减.
第二是考察到了相对速度不为零的两物体间的运动,此方面的题关键是要判断能否具有共同速度或在什么时间、位置上两物体具有共同速度.
对于圆周运动的问题,首先要经过受力分析表示出向心力,再结合各物理量表示的向心力的式子进行求解.

 中考解读考点精练系列答案
中考解读考点精练系列答案| A. | 法拉第提出了“电力线”的概念,认为电场强度的方向为电势降低的方向 | |
| B. | 法拉第指出:闭合电路中感应电动势的大小,跟穿过这一电路的磁通量的变化成正比 | |
| C. | 由楞次定律可知:感应电流的磁场总是要阻碍引起感应电流的磁通量的变化 | |
| D. | 由安培力公式可知:任意形状导线在匀强磁场中受到的安培力,可看作无限多直线电流元I△L在磁场中受到的安培力的矢量和 |
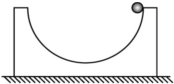 如图所示,内壁光滑的半圆形凹槽放置于粗糙的水平地面上,现将一个小铁球从与圆心等高处由静止释放,在铁球沿凹槽内壁下滑的过程中凹槽保持静止,则在铁球由最高点下滑到最低点的过程中,下列说法中正确的是( )
如图所示,内壁光滑的半圆形凹槽放置于粗糙的水平地面上,现将一个小铁球从与圆心等高处由静止释放,在铁球沿凹槽内壁下滑的过程中凹槽保持静止,则在铁球由最高点下滑到最低点的过程中,下列说法中正确的是( )| A. | 小球竖直方向的加速度逐渐增加 | |
| B. | 小球竖直方向的加速度逐渐减小 | |
| C. | 小球水平方向的加速度先增加后减小 | |
| D. | 小球水平方向的加速度先减小后增加 |
 如图所示,甲、乙是规格相同的灯泡.当接线柱a,b接电压为U的直流电源时,无论电源的正极与哪一个接线柱相连,甲灯均能正常发光,乙灯均不亮;当a,b接电压的有效值为U的交流电源时,甲灯发出微弱的光,乙灯能正常发光.关于与甲灯串联的元件x和与乙灯串联的元件y,下列判断正确的是( )
如图所示,甲、乙是规格相同的灯泡.当接线柱a,b接电压为U的直流电源时,无论电源的正极与哪一个接线柱相连,甲灯均能正常发光,乙灯均不亮;当a,b接电压的有效值为U的交流电源时,甲灯发出微弱的光,乙灯能正常发光.关于与甲灯串联的元件x和与乙灯串联的元件y,下列判断正确的是( )| A. | x可能是电感线圈,y可能是电容器 | B. | x可能是电容器,y可能是电感线圈 | ||
| C. | x可能是二极管,y可能是电容器 | D. | x可能是电感线圈,y可能是二极管 |
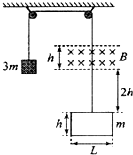 如图所示,质量为3m的重物与一质量为m的导线框用一根绝缘细线连接起来,挂在两个高度相同的定滑轮上,已知导线框电阻为R,横边边长为L.有一垂直纸面向里的匀强磁场,磁感应强度为B,磁场上下边界的距离、导线框竖直边长均为h.初始时刻,磁场的下边缘和导线框上边缘的高度差为2h,将重物从静止开始释放,导线框加速进入磁场,在导线框穿出磁场前已经做匀速直线运动,滑轮质量、摩擦阻力均不计,重力加速度为g.则下列说法中正确的是( )
如图所示,质量为3m的重物与一质量为m的导线框用一根绝缘细线连接起来,挂在两个高度相同的定滑轮上,已知导线框电阻为R,横边边长为L.有一垂直纸面向里的匀强磁场,磁感应强度为B,磁场上下边界的距离、导线框竖直边长均为h.初始时刻,磁场的下边缘和导线框上边缘的高度差为2h,将重物从静止开始释放,导线框加速进入磁场,在导线框穿出磁场前已经做匀速直线运动,滑轮质量、摩擦阻力均不计,重力加速度为g.则下列说法中正确的是( )| A. | 导线框刚进入磁场时的速度为v=2$\sqrt{gh}$ | |
| B. | 导线框进入磁场后,若某一时刻的速度为v,则此时重物的加速度为a=$\frac{1}{2}$g-$\frac{{B}^{2}{L}^{2}v}{4mR}$ | |
| C. | 导线框穿出磁场时的速度为$\frac{mgR}{{B}^{2}{L}^{2}}$ | |
| D. | 导线框通过磁场的过程中产生的热量Q=8mgh-$\frac{8{m}^{3}{g}^{2}{R}^{2}}{{B}^{4}{L}^{4}}$ |
| A. | 1W | B. | 10W | C. | 100W | D. | 1000W |
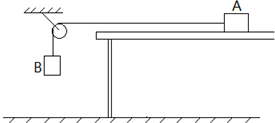 用如图所示的装置测量物块A与水平桌面间的动摩擦因数.将物块A置于水平桌面上,用轻绳绕过轻质定滑轮与物块B相连,不计绳子质量、不计绳与滑轮间的摩擦力、不计空气阻力.实验时将连接A的细绳调节至与桌面平行,按压住物块A使B物块自然悬垂,系统稳定后用米尺测出此时物块B距离地面的高度h,然后由静止释放A,B物块拉动A运动,B落地后即可停止,物块A继续在桌面上滑行一段距离后停在桌面上.为测出物块A与水平桌面间的动摩擦因数,本实验还需要测量的物理量是A、B的质量,滑块A运动的总距离,除米尺外还需要的测量仪器是天平,所测动摩擦因数的表达式为 μ=$\frac{{m}_{B}h}{({m}_{A}+{m}_{B})s+{m}_{B}h}$,式中各符号的意义是mA、mB分别为A、B的质量,s为滑块A运动的总距离.
用如图所示的装置测量物块A与水平桌面间的动摩擦因数.将物块A置于水平桌面上,用轻绳绕过轻质定滑轮与物块B相连,不计绳子质量、不计绳与滑轮间的摩擦力、不计空气阻力.实验时将连接A的细绳调节至与桌面平行,按压住物块A使B物块自然悬垂,系统稳定后用米尺测出此时物块B距离地面的高度h,然后由静止释放A,B物块拉动A运动,B落地后即可停止,物块A继续在桌面上滑行一段距离后停在桌面上.为测出物块A与水平桌面间的动摩擦因数,本实验还需要测量的物理量是A、B的质量,滑块A运动的总距离,除米尺外还需要的测量仪器是天平,所测动摩擦因数的表达式为 μ=$\frac{{m}_{B}h}{({m}_{A}+{m}_{B})s+{m}_{B}h}$,式中各符号的意义是mA、mB分别为A、B的质量,s为滑块A运动的总距离.