Question

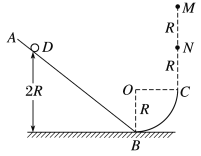
【题目】如图，水平地面上有一固定光滑斜面AB，其底端B点与半径为R的四分之一圆弧平滑连接，圆弧的端点C与圆心在同一水平线上，M、N为C点正上方两点，距离C点分别为2R和R，现将一小球从M点静止释放，小球在AB上能到达最高处D点距水平面的高度为2R，接着小球沿斜面滑下返回进入圆弧轨道，若不考虑空气阻力，则（ ）

A．小球返回轨道后沿轨道运动可能到不了C点

B．小球返回轨道后能沿轨道一直运动，并上升到N点

C．小球返回轨道后沿轨道运动到C点时，速度一定大于零

D．若将小球从N点静止释放，则小球在AB上能到达最高处距水平面的高度等于R

Answer 1

【答案】C

【解析】

试题分析：据题意可知，小球从M静止释放能到达D点，由能量关系可知在经过四分之一圆弧过程中损失的机械能为（小球在圆弧轨道上运动的速度越大，与轨道间的压力越大，摩擦力也就越大，摩擦力做功越多，损失的机械能也越多；同理速度越小摩擦力做功就越少，损失的机械能也就越少）；当小球从D点返回时，经过圆弧轨道的速度要小于从M点开始下落时经过圆弧轨道的速度，所以在返回过程中损失的机械能小于．故一定能到达C点，所以A错误。因为若返回过程中没有机械能损失的话恰好能回到N点，而现在有机械能损失所以不可能回到N点，故B错误。由于在返回过程中损失的能量小于，所以小球到达C点时速度一定大于零，所以C正确。若将小球从N点静止释放，小球能量小于，所以小球在AB上能到达最高处距水平面的高度h满足R＜h＜2R，所以D错误。