题目内容
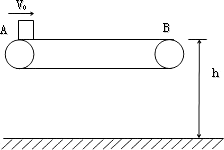
如图所示是长度为L=8．0 m的水平传送带，其皮带轮的半径为R=0．20 m，传送带上部距地面的高度为h=0．45m。质量m=4．0 kg的小物体A(视为质点)以v0=10m／s的初速度从左端滑上传送带。若传送带静止，A将从传送带水平部分最右端的B点滑落，落地点距B点的水平距离为0．6m。(g取10m／s2)(1)若皮带轮顺时针匀速转动，当皮带轮的角速度ω值在什么范围内，小物体落地点距B点的水平距离始终为0．6 m?
(2)若皮带轮以角速度ω=30rad／s顺时针匀速转动，A的落地点距B点的水平距离为多少?
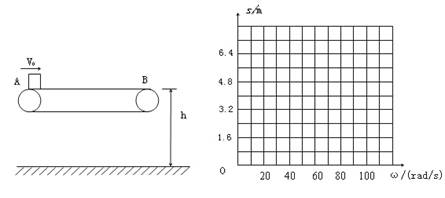
(3)皮带轮以不同的角速度顺时针匀速转动，画出A的落地点距B点的水平距离s随角速度ω变化的图像(ω的取值范围从0到100rad／s，不要求写出解析过程，只要画出的图线完全正确得5分)。
解：(1)设A与传送带间的动摩擦因数为μ，A从B点滑落时的速度为v，由平抛运动规律：x=vt h=
gt2 v=
=2m／s A落地点距B点的水平距离始终为0.6 m，即A离开传送带时的速度始终为2 m／s即ω≤10 rad／s
(2)当传送带静止时 由μmgL=
mv02-
mv2 得：μ=0.6 当皮带轮以角速度ω=30 rad／s顺时针匀速转动时，传送带的速度 v2=ωR=30×0.2=6 m／s 设A滑动s距离后与传送带相对静止μmgs=
mv02-
得：s=5.3m＜L
所以A与传送带相对静止后，以v2从B点平抛，落地点距B点的水平距离为x′=v2t=1.8m
(3)水平距离s随角速度ω变化的图像如图所示
附解析如下：当皮带轮以角速度10 rad／s＜ω＜50 rad／s 顺时针匀速转动时，A先在传送带上减速到与传送带相对静止后，以传送带的运行速度做平抛运动，传送带的速度v=ωR A落地点距月点的水平距离为：s=vt=0.06ω 设皮带轮以角速度ω′顺时针匀速转动时，A运动到B点时恰好与传送带相对静止μmgL=
mv32-
mv02，其中v1=ω′R 得：ω′=70rad／s 当皮带以角速度50 rad／s≤ω≤70 rad／s顺时针匀速转动时，A在传送带上加速到与传送带相对静止后，以传送带的运行速度平抛A落地点距B点的水平距离为：s=vt=0．060ω 当皮带轮以角速度70 rad/s＜ω≤100 rad／s顺时针匀速转动时，A在传送带上一直加速到B点，到达B点时的速度v4，μmgL=
mv42-
mv02 得：v4=14m／s A落地点距B点的水平距离为：s=vt=4.2 m
