题目内容
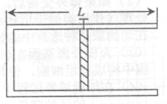
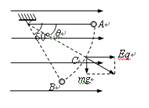
如图所示,用长L的绝缘细线拴住一只质量为m的、带电量为q的小球,线的另一端拴在水平向右的匀强电场中,开始时把小球、线拉到和O在同一水平面上(线拉直)A点,让小球由静止开始释放,当摆线摆到与水平线成60°角到达B点时,球的速度正好为零,求:
 (1)A、B两点之间的电势差。
(1)A、B两点之间的电势差。
(2)匀强电场的场强。
(3)小球运动到B点时细线上的拉力大小。
(4)分析小球到达B点以后的运动情况。
解:带电小球从A点到由静止释放摆到B点过程中重力做正功,但球由A到B时动能增量为零,因此电场力在这一过程中做负功,小球应带正电,由动能定理可以知道
(1)mglsin60°-Uq=0 ![]()
(2)![]()
(3)到达B位置时受电场力 ![]()
电场力F沿切线方向的分量斜向右上方与水平成30°角,大小为:
![]()
重力沿切线方向分量斜向左下方,大小为: ![]()
由于![]() 大于
大于![]() ,在B位置时小球不平衡,B位置小球对线的拉力不能用平衡条件∑F=0来求,只能根据球在沿线方向合力为零来求,设线上拉力为T,则:
,在B位置时小球不平衡,B位置小球对线的拉力不能用平衡条件∑F=0来求,只能根据球在沿线方向合力为零来求,设线上拉力为T,则:
T=Eqsin30°+mgsin60°=![]() mg
mg
(4)由于在B位置时,![]() =Eqsin30°=3mg/2大于
=Eqsin30°=3mg/2大于![]() =mgsin30°=mg/2,小球将沿圆弧向上运动,在A、B之间的圆弧上某点(设这时线与水平成θ角,如图)有Eqsinθ=mgcosθ,即:
=mgsin30°=mg/2,小球将沿圆弧向上运动,在A、B之间的圆弧上某点(设这时线与水平成θ角,如图)有Eqsinθ=mgcosθ,即:
![]()
![]() θ=30°
θ=30°
在θ=30°(即小球在C位置)时,小球切向合力为零,C位置为小球的平衡位置,所以小球到达B点以后会往回绕过C位置振动。

练习册系列答案
相关题目