题目内容
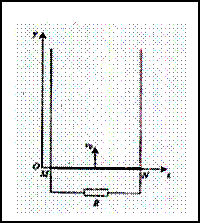
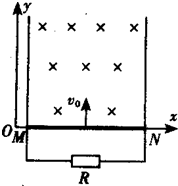如图，两根相距为d的足够长的光滑平行金属导轨位于竖直的xOy平面内，导轨与竖直轴Oy平行，其一端接有阻值为R的电阻．在y＞0的一侧整个平面内存在着与xOy平面垂直的匀强磁场，磁感应强度为B．一质量为m的金属直杆MN与金属导轨垂直，可在导轨上滑动，当t=0时金属杆MN位于y=0处，速度为v0，方向沿y轴的正方向．在MN向上运动的过程中，有一平行于y轴的拉力F作用于金属杆MN上，以保持其做匀速直线运动．设除电阻R外，所有其他电阻都可以忽略．问：（1）通过电阻R的电流为多少？方向如何？
（2）金属杆在向上运动的过程中拉力F的大小和方向如何？
分析：1、由E=BLv求出导体棒切割磁感线产生的感应电动势，由欧姆定律求出感应电流；
2、由F=BIL求出导体棒受到的安培力，然由平衡条件求出拉力．
2、由F=BIL求出导体棒受到的安培力，然由平衡条件求出拉力．
解答：解：（1）感应电动势为：
E=BLv=Bdv0
根据欧姆定律，通过电阻R的电流为：
I=
=
根据右手定则，感应电流的方向N→M，即通过R向右．
（2）根据左手定则，金属杆受到安培力竖直向下，有：
F=BId=B
d．
由于金属杆做匀速直线运动，根据平衡条件有：
F=mg+F安．
得：F=mg+
，方向竖直向上．
答：（1）通过电阻R的电流为
，方向向右．
（2）金属杆在向上运动的过程中拉力F的大小为mg+
，方向竖直向上．
E=BLv=Bdv0
根据欧姆定律，通过电阻R的电流为：
I=
| E |
| R |
| Bdv0 |
| R |
根据右手定则，感应电流的方向N→M，即通过R向右．
（2）根据左手定则，金属杆受到安培力竖直向下，有：
F=BId=B
| Bdv0 |
| R |
由于金属杆做匀速直线运动，根据平衡条件有：
F=mg+F安．
得：F=mg+
| B2d2v0 |
| R |
答：（1）通过电阻R的电流为
| Bdv0 |
| R |
（2）金属杆在向上运动的过程中拉力F的大小为mg+
| B2d2v0 |
| R |
点评：本题是电磁感应中受力平衡和简单电路的问题，基础是识别电路的结构，难度不大．
练习册系列答案
相关题目
如图所示，相距为d的两根直木棍AB和CD相互平行，斜靠在竖直墙壁上固定不动，两木棍与水平面的倾角均为θ，将一根横截面外径为
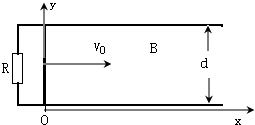如图所示，两根相距为d的足够长的平行金属导轨位于水平的xy平面内，一端接有阻值为R的电阻．在x＞0的一侧存在沿垂直纸面方向的均匀磁场，磁感强度B随x的增大而增大，B=kx，式中的k是一常量，一金属直杆与金属导轨垂直，可在导轨上无摩擦的滑动，当t=0时位于x=0处，速度为v0，方向沿x轴的正方向．在运动过程中，有一大小可调节的外力F作用于金属杆以保持金属杆的加速度恒定，大小为a，方向沿x轴的负方向．设除外接的电阻R外，所有其它电阻都可以忽略．
时，同路中的感应电动势多大?
时，闭合回路的感应电动势多大？此时作用于金属杆的外力F多大？