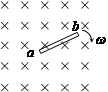题目内容
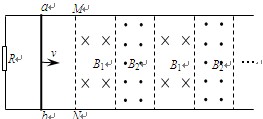
如图,相距L=1m、电阻不计的平行光滑长金属导轨固定在绝缘水平面上,两导轨左端间接有阻值R=2Ω的电阻,导轨所在区域内加上与导轨所在平面垂直、方向相反的匀强磁场,磁场宽度d均为0.6m,磁感应强度大小B1= T、B2=0.8T。现有电阻r=1Ω的导体棒ab垂直导轨放置且接触良好,当导体棒ab从边界MN进入磁场后始终以速度
T、B2=0.8T。现有电阻r=1Ω的导体棒ab垂直导轨放置且接触良好,当导体棒ab从边界MN进入磁场后始终以速度 m/s作匀速运动,求:
m/s作匀速运动,求:
⑴棒ab在磁场B1中时克服安培力做功的功率;
⑵棒ab经过任意一个磁场B2区域过程中通过电阻R的电量;
⑶棒ab在磁场中匀速运动时电阻R两端电压的有效值。
 T、B2=0.8T。现有电阻r=1Ω的导体棒ab垂直导轨放置且接触良好,当导体棒ab从边界MN进入磁场后始终以速度
T、B2=0.8T。现有电阻r=1Ω的导体棒ab垂直导轨放置且接触良好,当导体棒ab从边界MN进入磁场后始终以速度 m/s作匀速运动,求:
m/s作匀速运动,求:
⑴棒ab在磁场B1中时克服安培力做功的功率;
⑵棒ab经过任意一个磁场B2区域过程中通过电阻R的电量;
⑶棒ab在磁场中匀速运动时电阻R两端电压的有效值。
(1) (2)0.16C(3)2V
(2)0.16C(3)2V
 (2)0.16C(3)2V
(2)0.16C(3)2V试题分析:(1)在磁场B1中:
 (1分)
(1分)  (1分)
(1分) (1分)
(1分)  W (2分)
W (2分)⑵ 在磁场B2中:
 (1分)
(1分)  (1分)
(1分) 
 ="0.16C" (2分)
="0.16C" (2分)⑶设棒ab产生电动势的有效值为E
在磁场B1中产生的电动势
 =
= V (1分)
V (1分)在磁场B2中产生的电动势
 V (1分)
V (1分)回路在一个周期T内产生的焦耳热

 (2分)
(2分)解得:电动势的有效值
 =3V (1分)
=3V (1分)电阻R两端电压的有效值为
 V
V点评:导体棒切割磁感线产生感应电动势,闭合回路中有感应电流,因此由焦耳定律可求出电阻产生的热量.由安培力公式可得知拉力大小,从而算出拉力做的功.由于磁 场方向在变化,所以产生的感应电流方向也在变,因此根据法拉第电磁感应定律去算出电动势大小,再得出电流大小.而通过电阻的电量则由平均电流与时间的关系 得出.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目


 =30°、宽度L=1m的足够长的U形平行光滑金属导轨固定在磁感应强度B=1T、范围充分大的匀强磁场中,磁场方向垂直导轨平面斜向上.现用一平行导轨的牵引力F,牵引一根质量m=0.2kg、电阻R=1
=30°、宽度L=1m的足够长的U形平行光滑金属导轨固定在磁感应强度B=1T、范围充分大的匀强磁场中,磁场方向垂直导轨平面斜向上.现用一平行导轨的牵引力F,牵引一根质量m=0.2kg、电阻R=1 、垂直导轨的金属棒ab,由静止沿导轨向上移动(ab棒始终与导轨接触良好且垂直,不计导轨电阻及一切摩擦)。问:
、垂直导轨的金属棒ab,由静止沿导轨向上移动(ab棒始终与导轨接触良好且垂直,不计导轨电阻及一切摩擦)。问: