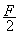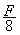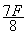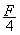题目内容
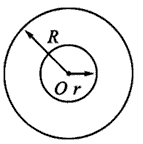
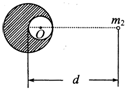 一个质量均匀分布的球体,半径为2r,在其内部挖去一个半径为r的球形空穴,其表面与球面相切,如图所示.已知挖去小球的质量为m,在球心和空穴中心连线上,距球心d=6r处有一个质量为m2的质点,求剩余部分对m2的万有引力?
一个质量均匀分布的球体,半径为2r,在其内部挖去一个半径为r的球形空穴,其表面与球面相切,如图所示.已知挖去小球的质量为m,在球心和空穴中心连线上,距球心d=6r处有一个质量为m2的质点,求剩余部分对m2的万有引力?分析:用没挖之前球对质点的引力,减去被挖部分对质点的引力,就是剩余部分对质点的引力.
解答:解:
由万有引力表达式:F=G
,由其内部挖去一个半径为r的球形空穴,挖去小球的质量为m,可知球体密度为:ρ=
.挖去之前的求的质量为M,则:M=
×
=8m,故挖去前的引力为:F=G
=
被挖部分对质点的引力为:F′=G
=
,剩余部分的引力为:F-F′=
-
=
答:剩余部分对m2的万有引力为
由万有引力表达式:F=G
| Mm |
| r2 |
| m | ||
|
| m | ||
|
| 4π(2r)3 |
| 3 |
| 8mm2 |
| (6r)2 |
| 2Gmm2 |
| 9r2 |
被挖部分对质点的引力为:F′=G
| mm2 |
| (5r)2 |
| Gmm2 |
| 25r2 |
| 2Gmm2 |
| 9r2 |
| Gmm2 |
| 25r2 |
| 41Gmm2 |
| 225r2 |
答:剩余部分对m2的万有引力为
| 41Gmm2 |
| 225r2 |
点评:本题的关键就是要对挖之前的引力和挖去部分的引力计算,而不是直接去计算剩余部分的引力,因为那是一个不规则球体,其引力直接由公式得到.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 如图,OA是一根长为L=0.3m的轻质硬杆,其一端通过光滑铰链与竖直光滑墙面连接,另一端A固定一质量均匀分布的球B,O′点为球心,O、A、O′三点在一条直线上,B球半径为r=0.2m,质量为M=3.0kg.矩形物块C的厚度为d=0.1m,质量为m=2.0kg,物块与球面间的动摩擦因数为μ=0.4.现在物块下端施加一个竖直向上、大小为20N的力F,使物块保持静止.g取10m/s2.求:
如图,OA是一根长为L=0.3m的轻质硬杆,其一端通过光滑铰链与竖直光滑墙面连接,另一端A固定一质量均匀分布的球B,O′点为球心,O、A、O′三点在一条直线上,B球半径为r=0.2m,质量为M=3.0kg.矩形物块C的厚度为d=0.1m,质量为m=2.0kg,物块与球面间的动摩擦因数为μ=0.4.现在物块下端施加一个竖直向上、大小为20N的力F,使物块保持静止.g取10m/s2.求: 如图,OA是一根长为L=0.3m的轻质硬杆,其一端通过光滑铰链与竖直光滑墙面连接,另一端A固定一质量均匀分布的球B,O′点为球心,O、A、O′三点在一条直线上,B球半径为r=0.2m,质量为M=3.0kg.矩形物块C的厚度为d=0.1m,质量为m=2.0kg,物块与球面间的动摩擦因数为μ=0.4.现在物块下端施加一个竖直向上、大小为30N的力F,使物块保持静止.g=10m/s2.求:
如图,OA是一根长为L=0.3m的轻质硬杆,其一端通过光滑铰链与竖直光滑墙面连接,另一端A固定一质量均匀分布的球B,O′点为球心,O、A、O′三点在一条直线上,B球半径为r=0.2m,质量为M=3.0kg.矩形物块C的厚度为d=0.1m,质量为m=2.0kg,物块与球面间的动摩擦因数为μ=0.4.现在物块下端施加一个竖直向上、大小为30N的力F,使物块保持静止.g=10m/s2.求: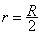 ,则原球体剩余部分对质点P的万有引力变为
,则原球体剩余部分对质点P的万有引力变为