题目内容
 (2012?天津)如图所示,水平地面上固定有高为h的平台,台面上有固定的光滑坡道,坡道顶端距台面也为h,坡道底端与台面相切.小球A从坡道顶端由静止开始滑下,到达水平光滑的台面后与静止在台面上的小球B发生碰撞,并粘连在一起,共同沿台面滑行并从台面边缘飞出,落地点与飞出点的水平距离恰好为台高的一半.两球均可视为质点,忽略空气阻力,重力加速度为g.求:
(2012?天津)如图所示,水平地面上固定有高为h的平台,台面上有固定的光滑坡道,坡道顶端距台面也为h,坡道底端与台面相切.小球A从坡道顶端由静止开始滑下,到达水平光滑的台面后与静止在台面上的小球B发生碰撞,并粘连在一起,共同沿台面滑行并从台面边缘飞出,落地点与飞出点的水平距离恰好为台高的一半.两球均可视为质点,忽略空气阻力,重力加速度为g.求:(1)小球A刚滑至水平台面的速度vA;
(2)A、B两球的质量之比mA:mB.
分析:(1)由动能定理或机械能守恒定律可以求出小球A刚滑到水平台面的速度.
(2)两小球碰撞过程中动量守恒,两小球离开平台后做平抛运动,
由动量守恒定律与平抛运动知识可以求出两球的速度之比.
(2)两小球碰撞过程中动量守恒,两小球离开平台后做平抛运动,
由动量守恒定律与平抛运动知识可以求出两球的速度之比.
解答:解:(1)小球A下滑过程中,由动能定理可得:
mAgh=
mAvA2-0,解得:vA=
;
(2)A、B两球碰撞时动量守恒,
由动量守恒定律可得:mAvA=(mA+mB)v,
离开平台后,两球做平抛运动,
水平方向:
=vt,
竖直方向:h=
gt2,
解得:mA:mB=1:3;
答:(1)小球A刚滑至水平台面的速度
;
(2)A、B两球的质量之比为mA:mB=1:3.
mAgh=
| 1 |
| 2 |
| 2gh |
(2)A、B两球碰撞时动量守恒,
由动量守恒定律可得:mAvA=(mA+mB)v,
离开平台后,两球做平抛运动,
水平方向:
| h |
| 2 |
竖直方向:h=
| 1 |
| 2 |
解得:mA:mB=1:3;
答:(1)小球A刚滑至水平台面的速度
| 2gh |
(2)A、B两球的质量之比为mA:mB=1:3.
点评:分析清楚运动过程,应用动能定理、动量守恒定律与平抛运动特点即可正确解题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
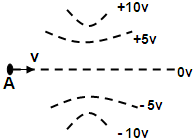 (2012?天津)两个固定的等量异号点电荷所产生电场等势面如图中虚线所示,一带负电的粒子以某一速度从图中A点沿图示方向进入电场在纸面内飞行,最后离开电场,粒子只受静电力作用,则粒子在电场中( )
(2012?天津)两个固定的等量异号点电荷所产生电场等势面如图中虚线所示,一带负电的粒子以某一速度从图中A点沿图示方向进入电场在纸面内飞行,最后离开电场,粒子只受静电力作用,则粒子在电场中( )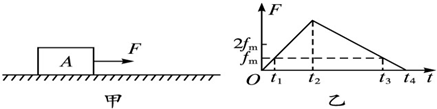 (2012?天津)如图甲所示,静止在水平地面的物块A,受到水平向右的拉力F作用,F与时间t的关系如图乙所示,设物块与地面的静摩擦力最大值fm与滑动摩擦力大小相等,则( )
(2012?天津)如图甲所示,静止在水平地面的物块A,受到水平向右的拉力F作用,F与时间t的关系如图乙所示,设物块与地面的静摩擦力最大值fm与滑动摩擦力大小相等,则( )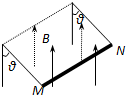 (2012?天津)如图所示,金属棒MN两端由等长的轻质细线水平悬挂,处于竖直向上的匀强磁场中,棒中通以由M向N的电流,平衡时两悬线与竖直方向夹角均为θ.如果仅改变下列某一个条件,θ角的相应变化情况是( )
(2012?天津)如图所示,金属棒MN两端由等长的轻质细线水平悬挂,处于竖直向上的匀强磁场中,棒中通以由M向N的电流,平衡时两悬线与竖直方向夹角均为θ.如果仅改变下列某一个条件,θ角的相应变化情况是( )