题目内容
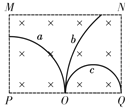
【题目】如图所示，两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上，a与转轴OO′的距离为l，b与转轴的距离为2l.木块与圆盘的最大静摩擦力为木块所受重力的k倍，重力加速度大小为g，若圆盘从静止开始绕转轴缓慢地加速转动，用ω表示圆盘转动的角速度．下列说法正确的是( )
A. b一定比a先开始滑动
B. a、b所受的摩擦力始终相等
C. ω＝
是b开始滑动的临界角速度
D. 当ω＝
时，a所受摩擦力的大小为kmg
【答案】AC
【解析】木块随圆盘一起转动，静摩擦力提供向心力，且两个木块的最大静摩擦力相等，当静摩擦力达到最大静摩擦时，开始滑动。牛顿第二定律得：木块所受的静摩擦力f=mω2r，而m、ω相等，所以r越大越先滑动，即b一定比a先开始滑动，故A正确；因为半径不同，由上可知需要的向心力不同，那么提供向心力得静摩擦力也不同，故B错误；对b为研究对象刚要滑动时有： 
，解得： 
，故C正确；对a为研究对象: 
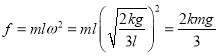，故D错误。所以AC正确，BD错误。
练习册系列答案
小题狂做系列答案
相关题目
