题目内容
如图所示,在圆锥形内部有三根固定的光滑细杆, A、B、C为圆锥底部同一圆周上的三个点,三杆Aa、bB、cC与水平底面的夹角分别为60o、45o、30o。每根杆上都套着一个小滑环(图中未画出),三个滑环分别从a、b、c处由静止释放(忽略阻力),用tl、t2、t3依次表示各滑环到达A、B、C所用的时间,则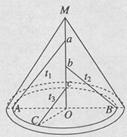
A.tl>t2>t3 B.t1 <t2< t3 C.tl=t3<t2 D.t1=t3> t2
D
解析试题分析:由牛顿第二定律可知滑环在杆上做初速度为0,加速度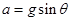 的匀加速直线运动,假设A、B、C三点所在圆的半径为
的匀加速直线运动,假设A、B、C三点所在圆的半径为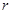 ,则
,则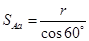 =2
=2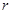 ,
,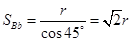 ,
,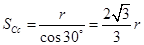 ,又根据匀变速直线运动公式
,又根据匀变速直线运动公式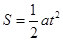 得
得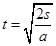 ,代入数据可知D正确,A、B、C错误。
,代入数据可知D正确,A、B、C错误。
考点:本题考查牛顿第二定律与匀变速直线运动的综合应用。

一质量为1kg的质点静止于光滑水平面上,从t=0时起,第1秒内受到2N的水平外力作用,第2秒内受到同方向的1N的外力作用。下列判断正确的是 ( )
| A.第1秒内的加速度为1m/s2 |
| B.第2秒内的位移为3m |
| C.2秒内外力做功为4.5J |
| D.2秒内外力做功的功率为2.5W |
某质点做匀变速直线运动,第3秒内的位移是6 m,第7秒内的位移是10m,则下列说法中正确的是
| A.质点的初速度是3.5 m/s |
| B.质点运动的加速度是1 m/s2 |
| C.质点运动的加速度是4 m/s2 |
| D.质点在4.5秒末的瞬时速度是8 m/s |
某物体做直线运动的位移与时间变化的关系式为x=4t+2t2,x与t的单位分别m和s,则物体的初速度和加速度分别是
| A.4m/s和2m/s2 | B.2m/s和2m/s2 |
| C.4m/s和4m/s2 | D.4m/s和1m/s2 |
甲、乙两物体先后从同一地点出发,沿一条直线运动,它们的v~t图象如图所示,由图可知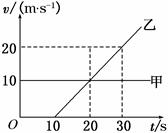
| A.甲比乙运动快,且早出发,所以乙追不上甲 |
| B.t="20" s时,乙追上了甲 |
| C.在t="20" s之前,甲比乙运动快;在t="20" s之后,乙比甲运动快 |
| D.由于乙在t="10" s时才开始运动,所以t="10" s时,甲在乙前面,它们之间的距离为乙追上甲前的最大距离 |
一个从静止开始做匀加速直线运动的物体,从开始运动起,连续通过三段位移的时间分别是1 s、2 s、3s,这三段位移的长度之比和这三段位移上的平均速度之比分别是( )
| A.1∶22∶32; 1∶2∶3 |
| B.1∶23∶33; 1∶22∶32 |
| C.1∶2∶3; 1∶1∶1 |
| D.1∶3∶5; 1∶2∶3 |
我国道路安全部门规定:高速公路上行驶的最高时速为120km/h。交通部门提供下列资料:
资料一:驾驶员的反应时间:0.3~0.6s
资料二:各种路面与轮胎之间的动摩擦因数
根据以上资料,可判断汽车行驶在高速公路上的安全距离最接近
| 路面 | 动摩擦因数 |
| 干沥青 | 0.7 |
| 干碎石路面 | 0.6~0.7 |
| 湿沥青 | 0.32~0.4 |
C.300m D.400m