题目内容
14.如图所示的模型中,小车放在光滑的水平轨道上,一切摩擦不计,小球的质量为m,小车质量为M,M=m,开始时小车静止,在甲、乙图中小球的初速度为v0,在丙图中小球的初速度为零,设甲图小球不能达到车的高度,乙图小球不能越过小车,丙图中圆弧半径为R,求小球上升的最大高度(离圆弧最低点的高度)各是多少?
分析 根据动量守恒定律可明确达最高点时的速度,再由机械能守恒定律可求得上升的高度.
解答 解:设向右为正方向,则对甲球,由动量守恒定律可知:
mv0=(M+m)v
由机械能守恒定律可知:
$\frac{1}{2}$mv02=$\frac{1}{2}$(M+m)v2+mgh
解得h=$\frac{m{{v}^{2}}_{0}}{2(M+m)g}=\frac{{{v}^{2}}_{0}}{4g}$;
对乙图可知:
mv0=(M+m)v
由机械能守恒定律可知:
$\frac{1}{2}$mv02=$\frac{1}{2}$(M+m)v2+mgh
解得:h=$\frac{m{{v}^{2}}_{0}}{2(M+m)g}=\frac{{{v}^{2}}_{0}}{4g}$;
对丙图设向右为正方向,由动量守恒可知:
小物体向上运动的过程中,m与M组成的系统在水平方向的动量守恒:
设小球滑至最高点时m与M的共同速度为v′
所以 mv=(M+m)v′
解得:$v′=\frac{m}{M+m}\sqrt{2gR}$
此过程中系统机械能守恒,所以
$\frac{1}{2}m{v}^{2}-\frac{1}{2}(M+m)v{′}^{2}=mgh$
解得m上升的最大高度:$h=\frac{M}{M+m}R$=$\frac{R}{2}$.
答:甲、乙两图中上升的高度均为$\frac{{v}_{0}^{2}}{4g}$;丙图中为$\frac{R}{2}$.
点评 本题考查动量守恒定律的应用及机械能守恒定律,要注意明确达最高点时的条件,正确选择正方向,才能可准确利用规律求解.

练习册系列答案
相关题目
5.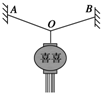 如图所示,为节日里悬挂灯笼的一种方式,A、B点等高,O为结点,轻绳AO、BO长度相等,∠AOB=120°,轻绳的拉力分别为FA、FB,灯笼受到的重力为G.下列说法正确的是( )
如图所示,为节日里悬挂灯笼的一种方式,A、B点等高,O为结点,轻绳AO、BO长度相等,∠AOB=120°,轻绳的拉力分别为FA、FB,灯笼受到的重力为G.下列说法正确的是( )
 如图所示,为节日里悬挂灯笼的一种方式,A、B点等高,O为结点,轻绳AO、BO长度相等,∠AOB=120°,轻绳的拉力分别为FA、FB,灯笼受到的重力为G.下列说法正确的是( )
如图所示,为节日里悬挂灯笼的一种方式,A、B点等高,O为结点,轻绳AO、BO长度相等,∠AOB=120°,轻绳的拉力分别为FA、FB,灯笼受到的重力为G.下列说法正确的是( )| A. | FA一定小于G | B. | FA与FB大小相等 | ||
| C. | FA与FB是一对平衡力 | D. | FA与FB大小之和等于G |
2.在大枣红了的时候,几个小朋友正在大枣树下用石块投向枣树,若某个小朋友从看到石块击中枣树树枝到听到大枣落地声最少需要0.7s,估算一下这课枣树的高度至少是( )
| A. | 1.5m | B. | 2.5m | C. | 5m | D. | 7m |
9.某电梯上升的速度图象如图所示,则( )


| A. | 前2s的平均速度是60m/s | B. | 第4s末的速度是60m/s | ||
| C. | 整过程的平均速度是45m/s | D. | 第6s末至第8s末电梯下降 |
19.关于自由落体运动,下列说法中正确的是( )
| A. | 无风的房间中将一根柔软的羽毛由静止释放,羽毛将做自由落体运动 | |
| B. | 自由落体运动一定是初速度为零、加速度为g的匀加速直线运动 | |
| C. | 质量大的物体,所受重力大,因而落地速度大 | |
| D. | 自由落体的加速度在地球赤道处最大 |
6. 如图所示,以直角三角形AOC为边界的有界匀强磁场区域,磁感应强度为B,∠A=60°,AO=a.在O点放置一个粒子源,可以向各个方向发射某种带负电粒子,粒子的比荷为$\frac{q}{m}$,发射速度大小都为v0,且满足v0=$\frac{qBa}{m}$,发射方向由图中的角度θ表示.对于粒子进入磁场后的运动(不计重力作用),下列说法正确的是( )
如图所示,以直角三角形AOC为边界的有界匀强磁场区域,磁感应强度为B,∠A=60°,AO=a.在O点放置一个粒子源,可以向各个方向发射某种带负电粒子,粒子的比荷为$\frac{q}{m}$,发射速度大小都为v0,且满足v0=$\frac{qBa}{m}$,发射方向由图中的角度θ表示.对于粒子进入磁场后的运动(不计重力作用),下列说法正确的是( )
 如图所示,以直角三角形AOC为边界的有界匀强磁场区域,磁感应强度为B,∠A=60°,AO=a.在O点放置一个粒子源,可以向各个方向发射某种带负电粒子,粒子的比荷为$\frac{q}{m}$,发射速度大小都为v0,且满足v0=$\frac{qBa}{m}$,发射方向由图中的角度θ表示.对于粒子进入磁场后的运动(不计重力作用),下列说法正确的是( )
如图所示,以直角三角形AOC为边界的有界匀强磁场区域,磁感应强度为B,∠A=60°,AO=a.在O点放置一个粒子源,可以向各个方向发射某种带负电粒子,粒子的比荷为$\frac{q}{m}$,发射速度大小都为v0,且满足v0=$\frac{qBa}{m}$,发射方向由图中的角度θ表示.对于粒子进入磁场后的运动(不计重力作用),下列说法正确的是( )| A. | 粒子有可能打到A 点 | |
| B. | 在AC 边界上只有一半区域有粒子射出 | |
| C. | 以θ=60°飞入的粒子在磁场中运动时间最短 | |
| D. | 以θ<30°飞入的粒子在磁场中运动的时间都相等 |
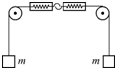 如图所示,两个弹簧测力计钩在一起,两边通过定滑轮各挂一个质量均为m的重物,则弹簧测力计的读数大小为( )
如图所示,两个弹簧测力计钩在一起,两边通过定滑轮各挂一个质量均为m的重物,则弹簧测力计的读数大小为( ) 如图所示,在倾角为37°的固定斜面上,有一个质量为5kg的物体静止放在斜面上,物体与斜面间的动摩擦因数μ为0.8.g取10m/s2,sin37°=0.6,cos37°=0.8,求:
如图所示,在倾角为37°的固定斜面上,有一个质量为5kg的物体静止放在斜面上,物体与斜面间的动摩擦因数μ为0.8.g取10m/s2,sin37°=0.6,cos37°=0.8,求: