题目内容
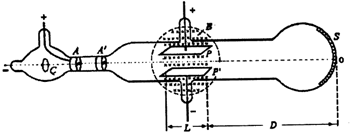 汤姆生用如图所示的装置(阴极射线管)发现了电子.电子由阴极C射出,在CA间电场加速,A′上有一小孔,所以只有一细束的电子可以通过P与P′两平行板间的区域,电子通过这两极板区域后打到管的末端,使末端S处的荧光屏发光(荧光屏可以近似看成平面).水平放置的平行板相距为d,长度为L,它的右端与荧光屏的距离为D.当平行板间不加电场和磁场时,电子水平打到荧光屏的O点;当两平行板间电压为U时,在荧光屏上S点出现一亮点,测出OS=H;当偏转板中又加一磁感应强度为B垂直纸面向里的匀强磁场时,发现电子又打到荧光屏的O点.若不考虑电子的重力,求
汤姆生用如图所示的装置(阴极射线管)发现了电子.电子由阴极C射出,在CA间电场加速,A′上有一小孔,所以只有一细束的电子可以通过P与P′两平行板间的区域,电子通过这两极板区域后打到管的末端,使末端S处的荧光屏发光(荧光屏可以近似看成平面).水平放置的平行板相距为d,长度为L,它的右端与荧光屏的距离为D.当平行板间不加电场和磁场时,电子水平打到荧光屏的O点;当两平行板间电压为U时,在荧光屏上S点出现一亮点,测出OS=H;当偏转板中又加一磁感应强度为B垂直纸面向里的匀强磁场时,发现电子又打到荧光屏的O点.若不考虑电子的重力,求(1)CA间的加速电压U′;
(2)电子的比荷
| e | m |
分析:(1)粒子在极板间时竖直方向做匀加速直线运动,射出偏转场后竖直方向做匀速直线运动,整个过程水平方向一直为匀速直线运动,利用竖直方向位移之和为H列方程求解;
(2)根据粒子所受电场力和洛伦兹力平衡列方程求比荷.
(2)根据粒子所受电场力和洛伦兹力平衡列方程求比荷.
解答:解:(1)粒子在加速场中:eU′=
mv02
得:U′=
①
偏转场中:a=
②
L=v0t1 ③
竖直方向位移:y1=
at12 ④
射出偏转场后,水平方向:D=v0t2 ⑤
竖直方向:y2=at1?t2 ⑥
又:y1+y2=H ⑦
联立②③④⑤⑥⑦得:
=
⑧
⑧代入①得:U′=
⑨
(2)当偏转板中又加一磁感应强度为B垂直纸面向里的匀强磁场时,发现电子又打到荧光屏的O点,根据平衡条件:
e
=ev0B ⑩
由①⑨⑩联立得:
=
答:(1)CA间的加速电压U′为
;(2)电子的比荷
=
.
| 1 |
| 2 |
得:U′=
| mv02 |
| 2e |
偏转场中:a=
| eU |
| md |
L=v0t1 ③
竖直方向位移:y1=
| 1 |
| 2 |
射出偏转场后,水平方向:D=v0t2 ⑤
竖直方向:y2=at1?t2 ⑥
又:y1+y2=H ⑦
联立②③④⑤⑥⑦得:
| mv02 |
| e |
| U(L2+2DL) |
| 2Hd |
⑧代入①得:U′=
| U(L2+2DL) |
| 4Hd |
(2)当偏转板中又加一磁感应强度为B垂直纸面向里的匀强磁场时,发现电子又打到荧光屏的O点,根据平衡条件:
e
| U |
| m |
由①⑨⑩联立得:
| e |
| m |
| 2HU |
| B2Ld(2D+L) |
答:(1)CA间的加速电压U′为
| U(L2+2DL) |
| 4Hd |
| e |
| m |
| 2HU |
| B2Ld(2D+L) |
点评:粒子在电场的偏转可运用平抛运动处理规律:将运动分解成相互垂直的两方向运动,因此将一个复杂的曲线运动分解成两个简单的直线运动,并用运动学公式来求解.

练习册系列答案
相关题目

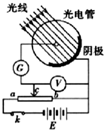 (1)用如图所示的装置研究光电效应现象,用光子能量为2.5eV的光照射到光电管上时,电流表G示数不为0,移动变阻器的触点c,当电压表的示数大于或等于时0.7V,电流表示数为0,则
(1)用如图所示的装置研究光电效应现象,用光子能量为2.5eV的光照射到光电管上时,电流表G示数不为0,移动变阻器的触点c,当电压表的示数大于或等于时0.7V,电流表示数为0,则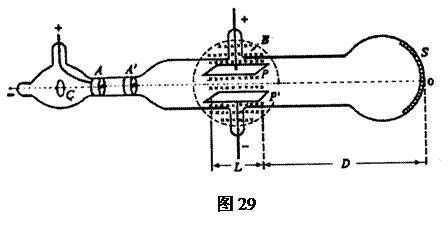
 (1)用如图所示的装置研究光电效应现象,用光子能量为2.5eV的光照射到光电管上时,电流表G示数不为0,移动变阻器的触点c,当电压表的示数大于或等于时0.7V,电流表示数为0,则______
(1)用如图所示的装置研究光电效应现象,用光子能量为2.5eV的光照射到光电管上时,电流表G示数不为0,移动变阻器的触点c,当电压表的示数大于或等于时0.7V,电流表示数为0,则______ Be+
Be+ He→
He→ C+
C+ n
n