题目内容
将地球看成是做匀速转动的圆球体，地球半径为6400km，则赤道上某点的线速度为v= m/s，角速度ω= rad/s．
分析：地球的自转周期，T=24h．赤道上的物体随地球自转，做匀速圆周运动，其周期等于地球自转周期．
根据角速度与周期的关系ω=
和线速度与周期的关系v=
，代入数据计算即可．
根据角速度与周期的关系ω=
| 2π |
| T |
| 2πR |
| T |
解答：解：赤道上的物体随地球自转，做匀速圆周运动，
其周期等于地球的自转周期，T=24h
所以ω=
=
rad/s≈7.27×10-5 rad/s
线速度的大小v=
=
m/s≈465.2m/s
故答案为：465.2；7.27×10-5．
其周期等于地球的自转周期，T=24h
所以ω=
| 2π |
| T |
| 2×3.14 |
| 24×3600 |
线速度的大小v=
| 2πR |
| T |
| 2×3.14×6400×103 |
| 24×3600 |
故答案为：465.2；7.27×10-5．
点评：本题考查角速度与周期的关系和线速度与周期的关系，同时要知道角速度与线速度的关系v=ωr．
练习册系列答案
阅读快车系列答案
相关题目
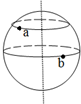如图所示，a、b是地球表面不同纬度上的两个点，把地球看作是一个匀速转动的球体，则这a、b两点一定具有相同的（ ）| A、线速度大小 | B、角速度 | C、线速度方向 | D、运动半径 |
如图所示，a、b是地球表面不同纬度上的两个点，把地球看作是一个匀速转动的球体，则这a、b两点一定具有相同的（ ）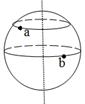
| A．线速度大小 | B．角速度 |
| C．线速度方向 | D．运动半径 |
＿＿＿＿ rad/s。