题目内容
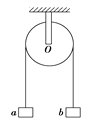
【题目】光滑水平桌面上,质量为m=1kg的木块(视为质点)左端与轻弹簧相连,弹簧的另一端固定。木块的右端与一轻细线连接,细线绕过光滑的质量不计的轻滑轮,木块开始静止在O点,弹簧处于原长。在细线的另一端施加一竖直向下的大小为F=10N的恒力,如图甲所示,木块从O点由静止开始向右运动。当木块运动至P点时,速度大小为v=1m/s,O、P两点间的距离为l =0.1m。(弹簧均处于弹性限度内,不计空气阻力和线的形变,重力加速度g取10m/s2。)
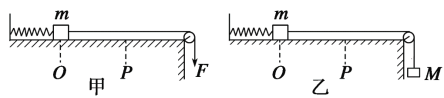
(1)求木块运动至P点时弹簧的弹性势能。
(2)如果在细线的另一端悬挂一个质量为M =3kg的重物,如图乙所示,木块从初始位置O由静止开始向右运动,求当木块通过P点时的速度大小。
(3)已知在弹性限度内,劲度系数为k,形变量为x时,弹簧的弹性势能为![]() 。在第(2)问给出的条件下,求出重物M由静止下落到最低点过程中的最大速度是多少?
。在第(2)问给出的条件下,求出重物M由静止下落到最低点过程中的最大速度是多少?
【答案】(1) 0.5J (2) ![]() m/s (3)1.5m/s
m/s (3)1.5m/s
【解析】
(1)用力F拉木块至P点时,设此时弹簧的弹性势能为![]() ,根据功能关系得:
,根据功能关系得:![]()
解得:![]()
(2)悬挂钩码M时,当木块运动到P点时,弹簧的弹性势能仍为![]() ,设木块的速度为
,设木块的速度为![]() ,由机械能守恒定律得:
,由机械能守恒定律得:![]()
解得:![]()
(3)根据:![]()
解得:![]()
当重物速度最大时,有:![]()
解得,当重物速度最大时,弹簧的伸长量:![]()
根据:![]() ,
,
解得,当重物速度最大时,弹簧的弹性势能:![]()
重物由开始下落到速度最大过程,由机械能守恒得:![]()
解得,重物的最大速度:![]()

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目