题目内容
12.相距很近的平行板电容器,在两板中心各开有一个小孔,如图甲所示,靠近A板的小孔处有一电子枪,能够持续均匀地发射出电子,电子的初速度为V0,质量为m,电量为-e,在AB两板之间加上图乙所示的交变电压,其中0<k<1,U0=$\frac{m{{v}_{0}}^{2}}{6e}$;紧靠B板的偏转电场电压也等于U0,板长为L,两板间距为d,距偏转极板右端$\frac{L}{2}$处垂直放置很大的荧光屏PQ.不计电子的重力和它们之间的相互作用,电子在电容器中的运动时间可以忽略不计.
(1)在0-T时间内,荧光屏上有两个位置会发光,试求这两个发光点之间的距离.(结果用L、d表示,第2小题亦然)
(2)只调整偏转电场极板的间距(仍以虚线为对称轴),要使荧光屏上只出现一个光点,极板间距应满足什么要求?
(3)撤去偏转电场及荧光屏,当k取恰当的数值,使在0-T时间内通过电容器B板的所有电子,能在某一时刻形成均匀分布的一段电子束,求k值.
分析 (1)在0-kT时间内,根据动能定理求出电子穿出B板后的速度,在偏转电场中,电子做类平抛运动,根据牛顿第二定律和运动学公式得到偏转距离.根据推论:电子射出偏转电场后,好像从“中点射出”,得到打在荧光屏上的坐标.再运用同样的方法求出在kT-T 时间内,电子打在荧光屏上的坐标,即可求得这两个发光点之间的距离.
(2)考虑到临界条件,当极板间距为d′时,电子刚从偏转极板边缘飞出,荧光屏上只出现一个光点,由上题结果求出极板间距应满足什么要求.
(3)要求在某一时刻形成均匀分布的一段电子束,前后两段电子束的长度必须相等,分别得到电子束长度的表达式,根据相等关系即可求得k.
解答 解:(1)电子经过电容器内的电场后,速度要发生变化.
在0-kT时间内,设穿出B板后速度变为v1,由动能定理得:
-eU0=$\frac{1}{2}$mv12-$\frac{1}{2}$mv02,
将U0=$\frac{m{{v}_{0}}^{2}}{6e}$
代入后解得:v1=$\sqrt{\frac{4e{U}_{0}}{m}}$.
在偏转电场中,电子运动时间t1=$\frac{L}{{v}_{1}}$,侧移量y1=$\frac{1}{2}$at12=$\frac{e{U}_{0}{L}^{2}}{2md{v}_{1}^{2}}$,
解得:y1=$\frac{{L}^{2}}{8d}$.
根据偏转电场中的推论“似是中点来”其打在荧光屏上的坐标y1′=2y1=$\frac{{L}^{2}}{4d}$
在kT-T 时间内,穿出B板后速度变为v2,同理可得,
v2=$\sqrt{\frac{8e{U}_{0}}{m}}$=$\sqrt{2}$v1,y2=$\frac{{L}^{2}}{16d}$.y2′=2y2=$\frac{{L}^{2}}{8d}$.
荧光屏上两个发光点之间的距离△y=y1′-y2′=$\frac{{L}^{2}}{8d}$.
(2)考虑到临界条件,当极板间距为d′时,电子刚从偏转极板边缘飞出,则有:
$\frac{1}{2}$d′=$\frac{1}{2}$a′t2,
又 a′=$\frac{F}{m}$=$\frac{e{U}_{0}}{md′}$,t=$\frac{L}{v}$
整理得,d′2=$\frac{e{U}_{0}{L}^{2}}{m{v}^{2}}$.
对于速度v1时,d1′=$\sqrt{\frac{e{U}_{0}{L}^{2}}{m{v}_{1}^{2}}}$=$\frac{1}{2}$L;
对于速度v2时,d2′=$\sqrt{\frac{e{U}_{0}{L}^{2}}{m{v}_{2}^{2}}}$=$\frac{\sqrt{2}}{4}$L;
只调整偏转电场极板的间距(仍以虚线为对称轴),要使荧光屏上只出现一个光点,极板间距应满足:$\frac{\sqrt{2}}{4}$L<d′<$\frac{1}{2}$L;
(3)要求在某一时刻形成均匀分布的一段电子束,前后两段电子束的长度必须相等(且刚好重叠),第一束长度:l1=v1•kT;第二束长度:l2=v2•(T-kT);
当l1= l2时,即v1•kT=$\sqrt{2}$v1•(1-k)T,
解得k=$\frac{\sqrt{2}}{\sqrt{2}+1}$≈0.59.
答:
(1)在0-T 时间内,荧光屏上有两个位置会发光,这两个发光点之间的距离是$\frac{{L}^{2}}{8d}$.
(2)只调整偏转电场极板的间距(仍以虚线为对称轴),要使荧光屏上只出现一个光点,极板间距应满足的要求是:L<d′<$\frac{1}{2}$L.
(3)撤去偏转电场及荧光屏,当k取恰当的数值,使在0-T 时间内通过电容器B 板的所有电子,能在某一时刻形成均匀分布的一段电子束,k值是0.59.
点评 本题利用带电粒子在匀强电场中的类平抛运动及其相关知识列方程进行解答,关键要分析出临界条件和隐含的条件.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 某人身系弹性绳自高空P点自由下落,图中a点是弹性绳的原长位置,c是人所到达的最低点,b是人静止地悬吊着时的平衡位置.不计空气阻力,则( )
某人身系弹性绳自高空P点自由下落,图中a点是弹性绳的原长位置,c是人所到达的最低点,b是人静止地悬吊着时的平衡位置.不计空气阻力,则( )| A. | 从P至c过程中重力所做的功与弹性绳弹力所做的功大小相等 | |
| B. | 从P至c过程中重力所做的功等于人克服弹力所做的功 | |
| C. | 从P至b过程中人的速度不断增大 | |
| D. | 从a至c过程中的加速度方向保持不变 |
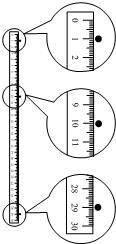 科技馆里有一个展品,该展品放在暗处,顶部有一个向下喷射水滴的装置,喷射水滴的时间间隔为△t.在频闪光源的照射下,可以看到水滴好像静止在空中固定的位置不动,如图所示.某同学为计算该装置喷射水滴的时间间隔,用最小刻度为毫米的刻度尺测量了空中几滴水间的距离,由此可计算出该装置喷射水滴的时间间隔△t为(g取10m/s2)( )
科技馆里有一个展品,该展品放在暗处,顶部有一个向下喷射水滴的装置,喷射水滴的时间间隔为△t.在频闪光源的照射下,可以看到水滴好像静止在空中固定的位置不动,如图所示.某同学为计算该装置喷射水滴的时间间隔,用最小刻度为毫米的刻度尺测量了空中几滴水间的距离,由此可计算出该装置喷射水滴的时间间隔△t为(g取10m/s2)( )| A. | 0.1s | B. | 0.2s | C. | 0.01s | D. | 0.02s |
| A. | 曲线运动是一种变速运动 | |
| B. | 曲线运动不可能是一种匀变速运动 | |
| C. | 做曲线运动的物体所受的合外力一定是变化的 | |
| D. | 做曲线运动的物体合外力可能为零 |
 如图所示,A、B是两个完全相同的金属小球,其中B固定在绝缘地板上,A在离地高H的正上方由静止释放下落,与B发生碰撞后回跳的高度为h,设碰撞中无机械能损失,空气阻力不计,则( )
如图所示,A、B是两个完全相同的金属小球,其中B固定在绝缘地板上,A在离地高H的正上方由静止释放下落,与B发生碰撞后回跳的高度为h,设碰撞中无机械能损失,空气阻力不计,则( )| A. | 若A、B带等量同种电荷,则h<H | B. | 若A、B带等量异种电荷,则h>H | ||
| C. | 若A、B带等量同种电荷,则h=H | D. | 若A、B带等量异种电荷,则h=H |