题目内容
3. 如图所示,长为L、质量为m的均质薄板AB的B端靠在竖直墙壁上,在距B端$\frac{3L}{4}$处支有一匀速转动的轮子,由于转动轮和板间摩擦力的作用,使AB板保持水平.已知B端与墙之间的最大静摩擦力为$\frac{2mg}{3}$.现有质量为m′=$\frac{m}{2}$的小物块以速度v0从A端水平滑上AB板,若物块与板间的动摩擦因数为μ,为使板依旧保持水平,物块初速度v0应取何值?
如图所示,长为L、质量为m的均质薄板AB的B端靠在竖直墙壁上,在距B端$\frac{3L}{4}$处支有一匀速转动的轮子,由于转动轮和板间摩擦力的作用,使AB板保持水平.已知B端与墙之间的最大静摩擦力为$\frac{2mg}{3}$.现有质量为m′=$\frac{m}{2}$的小物块以速度v0从A端水平滑上AB板,若物块与板间的动摩擦因数为μ,为使板依旧保持水平,物块初速度v0应取何值?
分析 根据力矩平衡求得小物块能滑到BC间的最大位置,据此算得小木块的最大位移,据运动规律求解物块的初速度.
解答 解:小物块最终停在离C点距离为x处右侧,根据力矩平衡条件有:
$mg(\frac{3L}{4}-\frac{L}{2})+m′gx={f}_{m}•\frac{3}{4}L$
代入m$′=\frac{m}{2}$和${f}_{m}=\frac{2mg}{3}$解得:
$x=\frac{L}{2}$
由此可知,物块在薄板上滑动的距离$s=\frac{L}{4}+x=\frac{3L}{4}$
物块在滑动摩擦力作用下做匀减速运动,根据牛顿第二定律有μm′g=ma
可得物块减速运动的加速度a=μg
据速度位移关系知,${v}^{2}-{v}_{0}^{2}=-2as$
可得${v}_{0}=\sqrt{2ax}$=$\sqrt{2×μg\frac{3L}{4}}$=$\sqrt{\frac{3μgL}{2}}$
答:物块初速度v0应取$\sqrt{\frac{3μgL}{2}}$.
点评 解决本题的关键是能根据木板平衡由力矩平衡条件求得物块的最终最大位置,再由运动学规律求得物块的位移和初速度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.下列说法正确的是( )
| A. | 电场中某一点的电场强度与放在该点的电荷有关 | |
| B. | 电荷在电场中某一点具有的电势能与该电荷无关 | |
| C. | 电场中某一点的电势只由电场本身决定,与放入电荷无关 | |
| D. | 电场中某两点间的电势差与零电势点选择有关 |
11. 嫦娥二号卫星由地面发射后,进入地月转移轨道,经多次变轨最终进入距离月球表面100公里,周期为118分钟的工作轨道,开始对月球进行探测,则下列说法错误的是( )
嫦娥二号卫星由地面发射后,进入地月转移轨道,经多次变轨最终进入距离月球表面100公里,周期为118分钟的工作轨道,开始对月球进行探测,则下列说法错误的是( )
 嫦娥二号卫星由地面发射后,进入地月转移轨道,经多次变轨最终进入距离月球表面100公里,周期为118分钟的工作轨道,开始对月球进行探测,则下列说法错误的是( )
嫦娥二号卫星由地面发射后,进入地月转移轨道,经多次变轨最终进入距离月球表面100公里,周期为118分钟的工作轨道,开始对月球进行探测,则下列说法错误的是( )| A. | 卫星在轨道Ⅲ上的运动速度比月球的第一宇宙速度小 | |
| B. | 卫星在轨道Ⅲ上运动周期比在轨道Ⅰ上小 | |
| C. | 卫星在轨道Ⅲ上经过P点的速度比在轨道Ⅰ上经过P点时大 | |
| D. | 卫星在轨道Ⅰ上经过P点的加速度等于在轨道Ⅱ上经过P点的加速度 |
18.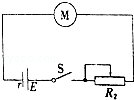 如图所示,电源电动势为E,内阻为r,电动机M的线圈电阻为R1.闭合开关S,电动机开始转动,稳定后电路中的电流为I,滑动变阻器接入电路的电阻为R2.则以下说法错误的是( )
如图所示,电源电动势为E,内阻为r,电动机M的线圈电阻为R1.闭合开关S,电动机开始转动,稳定后电路中的电流为I,滑动变阻器接入电路的电阻为R2.则以下说法错误的是( )
 如图所示,电源电动势为E,内阻为r,电动机M的线圈电阻为R1.闭合开关S,电动机开始转动,稳定后电路中的电流为I,滑动变阻器接入电路的电阻为R2.则以下说法错误的是( )
如图所示,电源电动势为E,内阻为r,电动机M的线圈电阻为R1.闭合开关S,电动机开始转动,稳定后电路中的电流为I,滑动变阻器接入电路的电阻为R2.则以下说法错误的是( )| A. | 电流大小I=$\frac{E}{{R}_{1}+{R}_{2}+r}$ | B. | 电动机两端的电压U=IR1 | ||
| C. | 电源的效率η=$\frac{{R}_{1}+{R}_{2}}{{R}_{1}+{R}_{2}+r}$×100% | D. | 电动机的机械功率P=IE-I2(R1+R2+r) |
8.用绿光做双缝干涉实验,在光屏上呈现出绿、暗相间的条纹,相邻两条绿条纹间的距离为△x.下列说法中正确的有( )
| A. | 如果增大单缝到双缝间的距离,△x将增大 | |
| B. | 如果增大双缝之间的距离,△x将增大 | |
| C. | 如果增大双缝到光屏之间的距离,△x将增大 | |
| D. | 如果将绿光换成波长更短的蓝光,其他条件不变,△x将增大 |
15.在以下各种说法中,正确的是( )
| A. | 一单摆做简谐运动,摆球相继两次通过同一位置时的速度必相同 | |
| B. | 横波在传播过程中,波峰上的质点运动到相邻的波峰所用的时间为一个周期 | |
| C. | 物体作受迫振动时的频率与它的固有频率无关,但若驱动力的频率等于其固有频率则会发生共振现象 | |
| D. | 如果测量到来自遥远星系上某些元素发出的光波波长比地球上这些元素静止时发光的波长长,这说明该星系正在远离我们而去 |
12. 为了节省能量,某商场安装了智能化的电动扶梯.无人乘行时,扶梯运转得很慢;有人站上扶梯时,它会先慢慢加速,再匀速运转.一顾客乘扶梯上楼,恰好经历了这两个过程,如图所示.那么下列说法中正确的是( )
为了节省能量,某商场安装了智能化的电动扶梯.无人乘行时,扶梯运转得很慢;有人站上扶梯时,它会先慢慢加速,再匀速运转.一顾客乘扶梯上楼,恰好经历了这两个过程,如图所示.那么下列说法中正确的是( )
 为了节省能量,某商场安装了智能化的电动扶梯.无人乘行时,扶梯运转得很慢;有人站上扶梯时,它会先慢慢加速,再匀速运转.一顾客乘扶梯上楼,恰好经历了这两个过程,如图所示.那么下列说法中正确的是( )
为了节省能量,某商场安装了智能化的电动扶梯.无人乘行时,扶梯运转得很慢;有人站上扶梯时,它会先慢慢加速,再匀速运转.一顾客乘扶梯上楼,恰好经历了这两个过程,如图所示.那么下列说法中正确的是( )| A. | 顾客先处于超重状态,后处于失重状态 | |
| B. | 顾客先受到三个力的作用,后受到二个力作用 | |
| C. | 顾客对扶梯作用力的方向先指向右下方,再竖直向下 | |
| D. | 顾客对扶梯作用力的方向先指向左下方,再竖直向下 |
 有一水平向右的匀强电场E=9.0×103N/C,在竖直平面内半径为0.1m的圆周上取上下左右四点A、B、C、D,在圆心O处放置带正电的点电荷Q=1.0×10-8C,则A处的场强大小为0N/C;D处的场强大小为9000$\sqrt{2}$N/C,方向向与水平成45°角斜向右上方.(k=9×109N•m2/C2)
有一水平向右的匀强电场E=9.0×103N/C,在竖直平面内半径为0.1m的圆周上取上下左右四点A、B、C、D,在圆心O处放置带正电的点电荷Q=1.0×10-8C,则A处的场强大小为0N/C;D处的场强大小为9000$\sqrt{2}$N/C,方向向与水平成45°角斜向右上方.(k=9×109N•m2/C2)