题目内容
7.如图甲所示,间距为L=0.3m、足够长的固定光滑平行金属导轨MN、PQ与水平面成θ=30°角,左端M、P之间连接有电流传感器和阻值为R=0.4Ω的定值电阻.导轨上垂直停放一质量为m=0.1kg、电阻为r=0.20Ω的金属杆ab,且与导轨接触良好,整个装置处于磁感应强度方向垂直导轨平面向下、大小为B=0.50T的匀强磁场中.在t=0时刻,用一与导轨平面平行的外力F斜向上拉金属杆ab,使之从由静止开始沿导轨平面斜向上做直线运动,电流传感器将通过R的电流i即时采集并输入电脑,可获得电流i随时间t变化的关系图线,如图乙所示.电流传感器和导轨的电阻及空气阻力均忽略不计,重力加速度大小为g=10m/s2.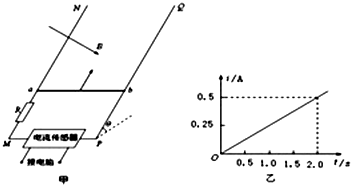
(1)求2s时刻杆ab的速度υ大小;
(2)求从静止开始在2秒内通过金属杆ab横截面的电量q;
(3)试证明金属杆做匀加速直线运动,并计算加速度a的大小.
分析 (1)根据2s时刻的电流通过闭合电路欧姆定律求出感应电动势,从而根据E=BLv求出杆ab的速度大小.
(2)根据法拉第电磁感应定律求出平均感应电动势,从而得出平均电流,根据q=It求出2秒内通过金属杆ab横截面的电量q.也可以通过I-t图线与时间轴所围成的面积表示电量进行求解.
(3)通过闭合电路欧姆定律,结合切割产生的感应电动势大小公式,推导出速度与时间的关系,看是否成正比关系,从而判断金属杆是否做匀加速直线运动.通过v=at得出加速度的大小.
解答 解:(1)设2s时刻的速度为v2,杆ab切割磁感线产生的感应电动势为:E=BLv2
根据闭合电路欧姆定律有:E=i( R+r )
由以上两式解得:v2=$\frac{i(R+r)}{BL}=\frac{0.5(0.4+0.2)}{0.5×0.3}m/s=2m/s$
(2)方法一:$q=\bar I△t=\frac{\bar E}{R+r}△t=\frac{BS}{△t(R+r)}△t=\frac{BS}{R+r}=\frac{{BL\frac{1}{2}a{t^2}}}{R+r}=0.5C$
方法二:由i-t图象可知:$q=\bar I△t=\frac{1}{2}×2.0×0.5C=0.5C$
(3)ab杆速度的表达式 v=$\frac{i(R+r)}{BL}=\frac{R+r}{BL}kt$;
因v与t是一次函数,故金属杆做匀加速直线运动,
其加速度大小a=$\frac{R+r}{BL}k=\frac{0.4+0.2}{0.5×0.3}×\frac{1}{4}m/{s^2}=1m/{s^2}$
答:
(1)2s时刻杆ab的速度υ大小为2m/s.
(2)从静止开始在2秒内通过金属杆ab横截面的电量q为0.5C.
(3)加速度a的大小为1m/s2.
点评 本题综合考查了法拉第电磁感应定律、闭合电路欧姆定律、牛顿第二定律等,得到v的表达式来分析杆的运动情况是关键.

 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案| A. | 布朗运动是液体分子的运动 | |
| B. | 布朗运动是悬浮微粒分子的运动 | |
| C. | 温度越高,布朗运动越显著 | |
| D. | 布朗微粒做无规则运动的原因是由于它受到水分子有时吸引、有时排斥的结果 |
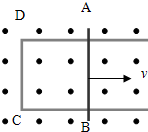 如图所示,导体AB是金属线框的一个可动边,AB与线框间无摩擦.匀强磁场垂直纸面向外.当AB以速度v向右做匀速运动时,下列说法中正确的是( )
如图所示,导体AB是金属线框的一个可动边,AB与线框间无摩擦.匀强磁场垂直纸面向外.当AB以速度v向右做匀速运动时,下列说法中正确的是( )| A. | 线框中的感应电流方向是A→B→C→D→A | |
| B. | 线框中的感应电流方向是A→D→C→B→A | |
| C. | 导体AB受到向右的磁场力 | |
| D. | 导体AB不受磁场力 |
| A. | 布朗运动证明分子在永不停息地做无规则热运动 | |
| B. | 热现象的微观理论认为,单个分子的运动是无规则的,但是大量分子的运动仍然有一定规律 | |
| C. | 已知水的摩尔质量和水分子的质量,就可以算出阿伏伽德罗常数 | |
| D. | 两个分子间由很远(r>10-9m)距离 减小到很难再靠近的过程中,分子间的作用力先减小后增大,分子势能不断增大 |
| A. | 物体的重力与地球对物体的万有引力是两种不同性质的力 | |
| B. | 人造地球卫星绕地球的向心力由地球对它的万有引力提供 | |
| C. | 人造地球卫星离地球越远,受到地球的万有引力越大 | |
| D. | 宇宙飞船内的宇航员处于失重状态是由于没有受到万有引力的作用 |
| A. | 电场强度反映了电场的力的性质,因此电场中某点的场强与检验电荷在该点所受的电场力成正比 | |
| B. | 电场中某点的场强等于$\frac{F}{q}$,但与检验电荷的受力大小及带电量无关 | |
| C. | 电场中某点的场强方向即正试探电荷在该点的受力方向 | |
| D. | 公式E=$\frac{F}{q}$和E=$\frac{kQ}{{r}^{2}}$对于任何静电场都是适用的 |
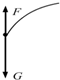
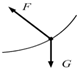
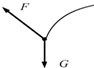
 如图所示,在一次救灾工作中,一架离水面高为H,沿水平直线飞行的直升机A,用悬索(重力可忽略不计)救护困在湖水中的伤员B,在直升机A和伤员B以相同的水平速度水平匀速运动的同时,悬索将伤员吊起.设经t时间后,A、B之间的距离为l,且l=H-t2,则在这段时间内关于伤员B的受力情况和运动轨迹描述正确的是下图中的哪个图( )
如图所示,在一次救灾工作中,一架离水面高为H,沿水平直线飞行的直升机A,用悬索(重力可忽略不计)救护困在湖水中的伤员B,在直升机A和伤员B以相同的水平速度水平匀速运动的同时,悬索将伤员吊起.设经t时间后,A、B之间的距离为l,且l=H-t2,则在这段时间内关于伤员B的受力情况和运动轨迹描述正确的是下图中的哪个图( )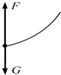
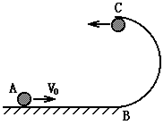 如图所示,光滑的水平轨道与光滑半圆弧轨道相切.圆轨道半径R=0.4m,一小球停放在光滑水平轨道上,现给小球一个v0=5m/s的初速度到c点的速度为3m/s.(g=10m/s2)
如图所示,光滑的水平轨道与光滑半圆弧轨道相切.圆轨道半径R=0.4m,一小球停放在光滑水平轨道上,现给小球一个v0=5m/s的初速度到c点的速度为3m/s.(g=10m/s2)