题目内容
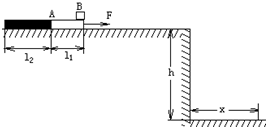 (2011?山东)如图所示,在高出水平地面h=1.8m的光滑平台上放置一质量M=2kg、由两种不同材料连接成一体的薄板A,其右段长度l1=0.2m且表面光滑,左段表面粗糙.在A最右端放有可视为质点的物块B,其质量m=1kg.B与A左段间动摩擦因数μ=0.4.开始时二者均静止,现对A施加F=20N水平向右的恒力,待B脱离A(A尚未露出平台)后,将A取走.B离开平台后的落地点与平台右边缘的水平距离x=1.2m.(取g=10m/s2)求
(2011?山东)如图所示,在高出水平地面h=1.8m的光滑平台上放置一质量M=2kg、由两种不同材料连接成一体的薄板A,其右段长度l1=0.2m且表面光滑,左段表面粗糙.在A最右端放有可视为质点的物块B,其质量m=1kg.B与A左段间动摩擦因数μ=0.4.开始时二者均静止,现对A施加F=20N水平向右的恒力,待B脱离A(A尚未露出平台)后,将A取走.B离开平台后的落地点与平台右边缘的水平距离x=1.2m.(取g=10m/s2)求(1)B离开平台时的速度vB.
(2)B从开始运动到刚脱离A时,B运动的时间tB和位移xB.
(3)A左端的长度l2.
分析:对A、B隔离受力分析,根据受力情况再做运动过程情况分析,根据运动性质结合物理规律解决问题.要注意物体运动的位移指的是相对于地面的位移.要善于画出运动过程的位置图象,有利于解题.
解答:解:(1)设物块平抛运动的时间为t,由平抛运动规律得:
h=
gt2,x=vBt
联立解得vB=2m/s.
(2)设B的加速度为aB,B在A的粗糙表面滑动,受向右的滑动摩擦力做匀加速直线运动.
由牛顿第二定律,F合=μmg=maB,
由匀变速直线运动规律,vB=aBtB,xB=
aBtB 2,
联立解得:tB=0.5s,xB=0.5m.
(3)设B刚好开始运动时A的速度为v,以A为研究对象,由动能定理得Fl1=
Mv12
设B运动后A的加速度为aA,由牛顿第二定律和运动学的知识得:
F-μmg=MaA,(l2+xB)=v1tB+
aAtB 2,
联立解得l2=1.5m.
答:(1)B离开平台时的速度vB为2m/s.
(2)B运动的时间tB为0.5s,位移xB为0.5m.
(3)A左端的长度l2为1.5m.
h=
| 1 |
| 2 |
联立解得vB=2m/s.
(2)设B的加速度为aB,B在A的粗糙表面滑动,受向右的滑动摩擦力做匀加速直线运动.
由牛顿第二定律,F合=μmg=maB,
由匀变速直线运动规律,vB=aBtB,xB=
| 1 |
| 2 |
联立解得:tB=0.5s,xB=0.5m.
(3)设B刚好开始运动时A的速度为v,以A为研究对象,由动能定理得Fl1=
| 1 |
| 2 |
设B运动后A的加速度为aA,由牛顿第二定律和运动学的知识得:
F-μmg=MaA,(l2+xB)=v1tB+
| 1 |
| 2 |
联立解得l2=1.5m.
答:(1)B离开平台时的速度vB为2m/s.
(2)B运动的时间tB为0.5s,位移xB为0.5m.
(3)A左端的长度l2为1.5m.
点评:能够根据物体的受力情况确定物体的运动情况,运用牛顿第二定律和运动学公式解决.动能定理的应用要注意过程的选取和总功的求解.

练习册系列答案
相关题目
 (2011?山东)如图所示,将两相同的木块a、b置于粗糙的水平地面上,中间用一轻弹簧连接,两侧用细绳固定于墙壁.开始时a、b均静止.弹簧处于伸长状态,两细绳均有拉力,a所受摩擦力Ffa≠0,b所受摩擦力Ffb=0,现将右侧细绳剪断,则剪断瞬间( )
(2011?山东)如图所示,将两相同的木块a、b置于粗糙的水平地面上,中间用一轻弹簧连接,两侧用细绳固定于墙壁.开始时a、b均静止.弹簧处于伸长状态,两细绳均有拉力,a所受摩擦力Ffa≠0,b所受摩擦力Ffb=0,现将右侧细绳剪断,则剪断瞬间( ) (2011?山东)如图所示,将小球a从地面以初速度v0竖直上抛的同时,将另一相同质量的小球b从距地面h处由静止释放,两球恰在
(2011?山东)如图所示,将小球a从地面以初速度v0竖直上抛的同时,将另一相同质量的小球b从距地面h处由静止释放,两球恰在 (2011?山东)如图所示,在两等量异种点电荷的电场中,MN为两电荷连线的中垂线,a、b、c三点所在直线平行于两电荷的连线,且a与c关于MN对称,b点位于MN上,d点位于两电荷的连线上.以下判断正确的是( )
(2011?山东)如图所示,在两等量异种点电荷的电场中,MN为两电荷连线的中垂线,a、b、c三点所在直线平行于两电荷的连线,且a与c关于MN对称,b点位于MN上,d点位于两电荷的连线上.以下判断正确的是( ) (2011?山东)如图所示,两固定的竖直光滑金属导轨足够长且电阻不计.两质量、长度均相同的导体棒c、d,置于边界水平的匀强磁场上方同一高度h处.磁场宽为3h,方向与导轨平面垂直.先由静止释放c,c刚进入磁场即匀速运动,此时再由静止释放d,两导体棒与导轨始终保持良好接触.用ac表示c的加速度,Ekd表示d的动能,xc、xd分别表示c、d相对释放点的位移.选项中正确的是( )
(2011?山东)如图所示,两固定的竖直光滑金属导轨足够长且电阻不计.两质量、长度均相同的导体棒c、d,置于边界水平的匀强磁场上方同一高度h处.磁场宽为3h,方向与导轨平面垂直.先由静止释放c,c刚进入磁场即匀速运动,此时再由静止释放d,两导体棒与导轨始终保持良好接触.用ac表示c的加速度,Ekd表示d的动能,xc、xd分别表示c、d相对释放点的位移.选项中正确的是( )