题目内容
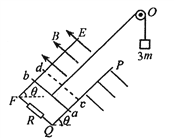
【题目】如图所示,两足够长的金属导轨EF、PQ倾斜固定,F、Q间接一阻值为R的电阻,其余部分电阻不计,两导轨间距为d,所在平面与水平面的夹角θ= 37°,导轨cd以上部分存在与导轨平面垂直的匀强磁场。转轴为0的光滑轻质定滑轮上跨轻质绝缘细线,一端系有质量为3m的重物,另一端系一质量为m、电阻不计的金属杆,开始时金属杆置于导轨上ab处,ab与cd距离为l0将重物从静止释放,当金属杆进入磁场时恰好做匀速直线运动。已知金属杆与导轨间的动摩擦因数μ= 0,5,ab运动过程中始终与导轨垂直,求:(取sin37°=0.6,cos37°= 0.8。重力加速度为g)
(1)金属杆进入磁场时的速率;
(2)匀强磁场磁感应强度的大小。
【答案】(1)![]() ;(2)
;(2)![]()
【解析】(1)金属杆进入磁场前,设重物和杆的加速度为a,细线上拉力大小为T:则3mg-t=3ma
T-mgsinθ-μmgcosθ=ma
金属杆进入磁场时的速度为vm:则![]()
解得: ![]()
(2)金属杆进入磁场时,电动势为E,电流为I,受安培力大小为F:则E=Bdvm
I=E∕R F=Bid
设细线上拉力大小为T0:3m-T0=0
T0-mgsinθ-μmgcosθ-F=0
解得![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目