题目内容
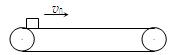
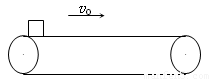
 如图,有一水平传送带以2m/s的速度匀速运动,现将一物体轻轻放在传送带的左端上,若物体与传送带间的动摩擦因数为0.5,已知传送带左、右端间的距离为10m,求传送带将该物体传送到传送带的右端所需时间.(g取10m/s2)
如图,有一水平传送带以2m/s的速度匀速运动,现将一物体轻轻放在传送带的左端上,若物体与传送带间的动摩擦因数为0.5,已知传送带左、右端间的距离为10m,求传送带将该物体传送到传送带的右端所需时间.(g取10m/s2)分析:先分析物体的运动情况:物体水平方向先受到滑动摩擦力,做匀加速直线运动;若传送带足够长,当物体速度与传送带相同时,物体做匀速直线运动.根据牛顿第二定律求出匀加速运动的加速度,由运动学公式求出物体速度与传送带相同时所经历的时间和位移,判断以后物体做什么运动,若匀速直线运动,再由位移公式求出时间.
解答:解:物体置于传动带左端时,先做加速直线运动,受力分析,由牛顿第二定律得:
f=μmg=ma
代入数据得:a=μg=0.5×10m/s2=5m/s2
当物体加速到速度等于传送带速度v=2m/s时,运动的时间为
t1=
=
s=0.4s
运动的位移s1=
=
m=0.4m<10m
则物体接着做匀速直线运动,匀速直线运动所用时间:
t2=
=
s=4.8s
所以物体传送到传送带的右端所需时间t=t1+t2=0.4s+4.8s=5.2s
答:传送带将该物体传送到传送带的右端所需时间为5.2s.
f=μmg=ma
代入数据得:a=μg=0.5×10m/s2=5m/s2
当物体加速到速度等于传送带速度v=2m/s时,运动的时间为
t1=
| v |
| a |
| 2 |
| 5 |
运动的位移s1=
| v2 |
| 2a |
| 22 |
| 2×5 |
则物体接着做匀速直线运动,匀速直线运动所用时间:
t2=
| s-s1 |
| v |
| 10-0.4 |
| 2 |
所以物体传送到传送带的右端所需时间t=t1+t2=0.4s+4.8s=5.2s
答:传送带将该物体传送到传送带的右端所需时间为5.2s.
点评:物体在传送带运动问题,关键是分析物体的受力情况,来确定物体的运动情况,有利于培养学生分析问题和解决问题的能力.

练习册系列答案
相关题目
 如图,有一水平传送带以2m/s的速度匀速运动,现将一物体轻轻放在传送带的左端上,若物体与传送带间的动摩擦因数为0.5,已知传送带左、右端间的距离为10m.
如图,有一水平传送带以2m/s的速度匀速运动,现将一物体轻轻放在传送带的左端上,若物体与传送带间的动摩擦因数为0.5,已知传送带左、右端间的距离为10m. 如图,有一水平传送带以2m/s的速度匀速运动,现将一物体轻轻放在传送带上,若物体与传送带间的动摩擦因数为0.5,则传送带将该物体传送10m的距离所需时间为多少?(g=10m/s2)
如图,有一水平传送带以2m/s的速度匀速运动,现将一物体轻轻放在传送带上,若物体与传送带间的动摩擦因数为0.5,则传送带将该物体传送10m的距离所需时间为多少?(g=10m/s2)