题目内容
如图所示，在水平方向的匀强电场（场强为E）中，在水平光滑桌面上有一半径为R的圆，O为圆心，AOB为一直径．现将一带正电q的微粒，以相同的动能从A点沿桌面射出，因射出方向不同，微粒将通过圆上的不同点，其中到达C点时微粒的动能最大．已知∠BAC=37°，则电场方向与AC的夹角θ=37°
37°
；若微粒从A点沿与电场垂直方向射出，微粒恰能通过C点，则射出时的初动能为0.18EqR
0.18EqR
．分析：1、小球在匀强电场中，从A点运动到C点，根据动能定理qUAC=Ek，因为到达C点时的小球的动能最大，所以UAC最大，即在圆周上找不到与C电势相等的点．所以与C点电势相等的点在过C点的切线上．再根据电场线与等势线垂直，可以画出电场线，从而确定电场方向与AC的夹角．
2、小球做类平抛运动，根据平抛运动的知识分析小球的运动情况，分别在水平方向和竖直方向上列式求解，从而根据动能定理，即可求解．
2、小球做类平抛运动，根据平抛运动的知识分析小球的运动情况，分别在水平方向和竖直方向上列式求解，从而根据动能定理，即可求解．
解答：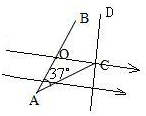
解：（1）小球在匀强电场中，从A点运动到C点，根据动能定理qUAC=Ek
因为到达C点时的小球的动能最大，所以UAC最大，即在圆周上找不到与C电势相等的点．且由A到C电场力对小球做正功．
过C点作切线，则CD为等势线．
过A点作CD的垂线，则该线为电场线，场强方向如图示．
∵∠BAC=37°，∴∠CAB=37°
而连接CO 则∠ACO=37°
所以电场方向与AC间的夹角θ为37°
（2）小球只受电场力，做类平抛运动．
水平方向上：x=Rcos37°=v0t
竖直方向上：y=R+Rsin37°=
由以上两式得：Ek=
mv2=0.18qER
故答案为：37°；0.18EqR．
解：（1）小球在匀强电场中，从A点运动到C点，根据动能定理qUAC=Ek因为到达C点时的小球的动能最大，所以UAC最大，即在圆周上找不到与C电势相等的点．且由A到C电场力对小球做正功．
过C点作切线，则CD为等势线．
过A点作CD的垂线，则该线为电场线，场强方向如图示．
∵∠BAC=37°，∴∠CAB=37°
而连接CO 则∠ACO=37°
所以电场方向与AC间的夹角θ为37°
（2）小球只受电场力，做类平抛运动．
水平方向上：x=Rcos37°=v0t
竖直方向上：y=R+Rsin37°=
| qEt2 |
| 2m |
由以上两式得：Ek=
| 1 |
| 2 |
故答案为：37°；0.18EqR．
点评：本题关键考查对电场力做功公式W=qEd的理解和应用，d是沿电场方向两点间的距离．此题要求熟练掌握功能关系和类平抛运动，属于难题．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
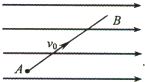如图所示，在水平方向的匀强电场中，一初速度为v0的带电微粒沿着竖直平面内的直线由A点运动到B点的过程中，微粒的（ ）| A、电势能一定减少，动能一定减少 | B、电势能一定增加，动能一定增加 | C、电势能一定减少，动能一定增加 | D、电势能一定增加，动能一定减少 |
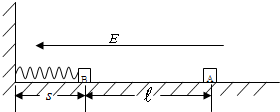（2008?揭阳二模）在绝缘水平面上，放一质量为m=2.0×10-3kg的带正电滑块A，所带电量为q=1.0×10-7C，在滑块A的左边?处放置一个不带电、质量M=4.0×10-3kg的绝缘滑块B，B的左端接触（不连接）于固定在竖直墙壁的轻弹簧上，轻弹簧处于自然状态，弹簧原长s=0.05m，如图所示．在水平方向加一水平向左的匀强电场，电场强度的大小为E=4.0×105N/C，滑块A由静止释放后向左滑动并与滑块B发生碰撞，设碰撞时间极短，碰撞后结合在一起共同运动的速度为v=1m/s，两物体一起压缩弹簧至最短处（弹性限度内）时，弹簧的弹性势能E0=3.2×10-3J．设两滑块体积大小不计，与水平面间的动摩擦因数为μ=0.50，摩擦不起电，碰撞不失电，g取10m/s2．求：
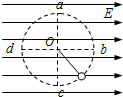（2009?南通模拟）如图所示，在水平方向的匀强电场中，绝缘细线的一端固定在O点，另一端系一带正电的小球在竖直平面内做圆周运动，小球所受电场力大小等于重力大小．则（ ）
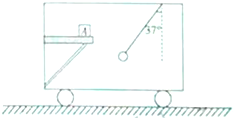如图所示，在水平方向上加速前进的车厢中，挂着小球的悬线与竖直方向成37°角，放在车厢里的水平桌面上的物体A相对桌面静止不动，若A的质量为1.0kg，取g=10m/s2，sin37°=0.6，cos37°=0.8．求：