题目内容
【题目】图中给出一段“ ![]() ”形单行盘山公路的示意图,弯道1、弯道2可看作两个不同水平面上的圆弧,圆心分别为
”形单行盘山公路的示意图,弯道1、弯道2可看作两个不同水平面上的圆弧,圆心分别为 ![]() ,弯道中心线半径分别为
,弯道中心线半径分别为 ![]() ,弯道2比弯道1高
,弯道2比弯道1高 ![]() ,有一直道与两弯道圆弧相切。质量
,有一直道与两弯道圆弧相切。质量 ![]() 的汽车通过弯道时做匀速圆周运动,路面对轮胎的最大径向静摩擦力是车重的1.25倍,行驶时要求汽车不打滑。(sin37°=0.6,sin53°=0.8)
的汽车通过弯道时做匀速圆周运动,路面对轮胎的最大径向静摩擦力是车重的1.25倍,行驶时要求汽车不打滑。(sin37°=0.6,sin53°=0.8)
(1)求汽车沿弯道1中心线行驶时的最大速度 ![]() ;
;
(2)汽车以 ![]() 进入直道,以
进入直道,以 ![]() 的恒定功率直线行驶了
的恒定功率直线行驶了 ![]() ,进入弯道2,此时速度恰为通过弯道2中心线的最大速度,求直道上除重力以外的阻力对汽车做的功;
,进入弯道2,此时速度恰为通过弯道2中心线的最大速度,求直道上除重力以外的阻力对汽车做的功;
(3)汽车从弯道1的A点进入,从同一直径上的B点驶离,有经验的司机会利用路面宽度,用最短时间匀速安全通过弯道,设路宽 ![]() ,求此最短时间(A、B两点都在轨道的中心线上,计算时视汽车为质点 )。
,求此最短时间(A、B两点都在轨道的中心线上,计算时视汽车为质点 )。
【答案】
(1)
弯道1的最大速度v1,有: ![]()
得 ![]()
(2)
弯道2的最大速度v2,有: ![]()
得 ![]()
直道上由动能定理有: ![]()
代入数据可得 ![]()
(3)![]()
可知r增大v增大,r最大,切弧长最小,对应时间最短,所以轨迹设计应如下图所示
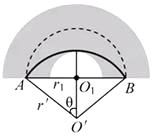
由图可以得到 ![]()
代入数据可以得到r’=12.5m
汽车沿着该路线行驶的最大速度 ![]()
![]()
由 ![]()
线路长度 ![]()
最短时间 ![]() 。
。
【解析】(1)汽车拐弯时靠静摩擦力提供向心力,当静摩擦力达到最大时,汽车的速度最大,根据牛顿第二定律求出汽车沿弯道1中心线行驶时的最大速度v1;(2)同理求出汽车沿弯道2中心线行驶时的最大速度v2,再研究汽车在直道上行驶的过程,运用动能定理求阻力对汽车做的功;(3)当汽车沿着与弯道1内切的弧线运动时时间最短,且速度最大,根据几何关系求出该弧线的半径,结合运动学公式求最短时间.
【考点精析】通过灵活运用静摩擦力和向心力,掌握静摩擦力:静摩擦力大小可在0与fmax 之间变化,一般应根据物体的运动状态由平衡条件或牛顿定律来求解;向心力总是指向圆心,产生向心加速度,向心力只改变线速度的方向,不改变速度的大小;向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时,千万不可在物体受力之外再添加一个向心力即可以解答此题.

【题目】游船从码头沿直线行驶到湖对岸,小明对过程进行观察,记录数据如下表,
运动过程 | 运动时间 | 运动状态 |
匀加速运动 |
| 初速度 |
匀速运动 |
|
|
匀减速运动 |
| 靠岸时的速度 |
(1)求游船匀加速运动过程中加速度大小 ![]() ,及位移大小
,及位移大小 ![]() ;
;
(2)若游船和游客总质量 ![]() ,求游船匀减速运动过程中所受合力的大小F;
,求游船匀减速运动过程中所受合力的大小F;
(3)求游船在整个行驶过程中的平均速度大小 。