题目内容
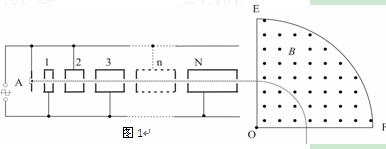
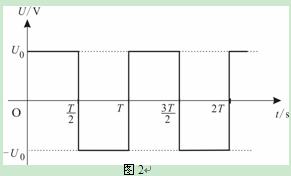
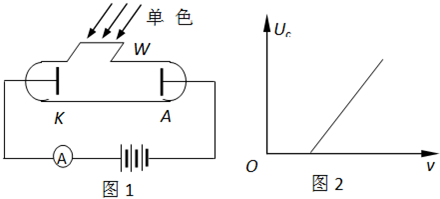
在图1所示的装置中，K为一金属板，A为金属电极，都密封在真空的玻璃管中，W为由石英片封盖的窗口，单色光可通过石英片射到金属板K上，E为输出电压可调的直流电流，其负极与电极A相连，
是电流表，实验发现，当用某种频率的单色光照射K时，K会发出电子（光电效应），这时，即使A、K之间的电压等于零，回路中也有电流．当A的电势低于K时，当A比K的电势低到某一值Uc时，电流消失，Uc称为截止电压，当改变照射光的频率ν，截止电压Uc也将随之改变，其关系如图2所示，如果某次实验我们测出了画出这条图线所需的一系列数据，又知道了电子电量，则 （ ）
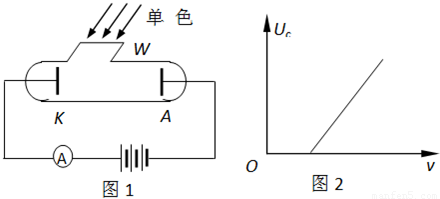
①可求得该金属的极限频率
②可求得该金属的逸出功
③可求得普朗克常量
④可求得中子的质量．
A．①②③④
B．②③
C．①③④
D．①②③
【答案】分析：根据光电效应方程得出遏止电压与入射光频率的关系，从而确定能够求出的物理量．
解答：解：根据光电效应方程得，Ekm=hv-W．因为最大初速度与遏止电压的关系为：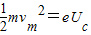
．则eUC=hv-W，所以
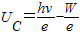．知图线的斜率k=
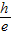，通过斜率可以求出普朗克常量．当UC=0时，hv=W，可得极限频率
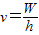，即横轴截距．从而可以求出逸出功．中子的质量无法求出．故D正确，A、B、C错误．
故选D．
点评：解决本题的关键掌握光电效应方程，知道遏止电压与最大初动能的关系．
解答：解：根据光电效应方程得，Ekm=hv-W．因为最大初速度与遏止电压的关系为：
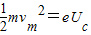．则eUC=hv-W，所以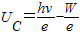．知图线的斜率k=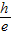，通过斜率可以求出普朗克常量．当UC=0时，hv=W，可得极限频率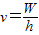，即横轴截距．从而可以求出逸出功．中子的质量无法求出．故D正确，A、B、C错误．故选D．
点评：解决本题的关键掌握光电效应方程，知道遏止电压与最大初动能的关系．
练习册系列答案
相关题目
是电流表，实验发现，当用某种频率的单色光照射K时，K会发出电子（光电效应），这时，即使A、K之间的电压等于零，回路中也有电流．当A的电势低于K时，当A比K的电势低到某一值Uc时，电流消失，Uc称为截止电压，当改变照射光的频率ν，截止电压Uc也将随之改变，其关系如图2所示，如果某次实验我们测出了画出这条图线所需的一系列数据，又知道了电子电量，则 （ ）
的正离子沿轴线进入一系列共轴且长度依次增加的金属圆筒，奇数和偶数筒分别连接在周期为T、最大值为U0的矩形波电源两端，电源波形如图2所示，离子在每个圆筒内做匀速直线运动的时间等于交变电源的半个周期，在相邻两筒之间受电场力作用被加速（加速时间不计）.离子离开最后一个圆筒后垂直于边OE进入磁感应强度为B的匀强磁场，最后从 OF边出射.（不计离子所受重力）
的离子也能垂直于OF边出射，求电源电压最
以及磁感应强度的改变量
.
