题目内容
 固定在水平地面上光滑斜面倾角为θ.斜面底端固定一个与斜面垂直的挡板,一木板A被放在斜面上,其下端离地面高为H,上端放着一个小物块B,如图所示.木板和物块的质量均为m.相互间最大静摩擦力等于滑动摩擦力kmgsinθ(k>1),把它们由静止释放,木板与挡板发生碰撞时,时间极短,无动能损失,而物块不会与挡板发生碰撞.求:
固定在水平地面上光滑斜面倾角为θ.斜面底端固定一个与斜面垂直的挡板,一木板A被放在斜面上,其下端离地面高为H,上端放着一个小物块B,如图所示.木板和物块的质量均为m.相互间最大静摩擦力等于滑动摩擦力kmgsinθ(k>1),把它们由静止释放,木板与挡板发生碰撞时,时间极短,无动能损失,而物块不会与挡板发生碰撞.求:(1)木板第一次与挡板碰撞弹回沿斜面上升过程中,物块B的加速度a1大小和方向;
(2)从释放木板到木板与挡板第二次碰撞的瞬间,木板A运动的路程s;
(3)从释放木板到木板和物块都静止,木板和物块系统损失的机械能E0.
分析:(1)木板上升时,对物块受力分析,在沿斜面方向上由牛顿运动定律列式求解,便可求出物块的加速度.
(2)此题要分段进行计算,第一段是木板开始下落直至第一次与挡板碰撞的过程,由几何关系可求出此过程的路程为
,第二段是从第一次与挡板碰撞到第一次运动到最高点,第三段是从最高点下落到第二次与挡板碰撞,后两段路程相同.可由牛顿运动定律和运动学公式求得.
(3)损失机械能等于阻力所做的功.
(2)此题要分段进行计算,第一段是木板开始下落直至第一次与挡板碰撞的过程,由几何关系可求出此过程的路程为
| H |
| sinθ |
(3)损失机械能等于阻力所做的功.
解答:解:(1)、木板第一次上升过程中,对物块受力分析,受到竖直向下的重力、垂直于斜面的支持力和沿斜面向上的摩擦力作用,设物块的加速度为a物块,
则物块受合力 F物块=kmgsinθ-mgsinθ…①
由牛顿第二定律 F物块=ma物块…②.
联立①②得:a物块=(k-1)gsinθ,方向沿斜面向上.
(2)设以地面为零势能面,木板第一次与挡板碰撞时的速度大小为v1,由机械能守恒有:
×2
=2mgH
解得:v1=
.
设木板弹起后的加速度a板,由牛顿第二定律有:
a板=-(k+1)gsinθ
S板第一次弹起的最大路程:S1=
解得:S1=
木板运动的路程S=
+2S1=
(3)设物块相对木板滑动距离为L
根据能量守恒有:mgH+mg(H+Lsinθ)=kmgsinθL
损失机械能 E0=fL=kmgsinθL
解得 E0=
答:(1)木板第一次与挡板碰撞弹回沿斜面上升过程中,物块B的加速度a1大小是(k-1)gsinθ,方向沿斜面向上;
(2)从释放木板到木板与挡板第二次碰撞的瞬间,木板A运动的路程是
;
(3)从释放木板到木板和物块都静止,木板和物块系统损失的机械能是
.
则物块受合力 F物块=kmgsinθ-mgsinθ…①
由牛顿第二定律 F物块=ma物块…②.
联立①②得:a物块=(k-1)gsinθ,方向沿斜面向上.
(2)设以地面为零势能面,木板第一次与挡板碰撞时的速度大小为v1,由机械能守恒有:
| 1 |
| 2 |
| mv | 2 1 |
解得:v1=
| 2gH |
设木板弹起后的加速度a板,由牛顿第二定律有:
a板=-(k+1)gsinθ
S板第一次弹起的最大路程:S1=
| ||
| 2a板 |
解得:S1=
| H |
| (k+1)sinθ |
木板运动的路程S=
| H |
| sinθ |
| (k+3)H |
| (k+1)sinθ |
(3)设物块相对木板滑动距离为L
根据能量守恒有:mgH+mg(H+Lsinθ)=kmgsinθL
损失机械能 E0=fL=kmgsinθL
解得 E0=
| 2kmgH |
| k-1 |
答:(1)木板第一次与挡板碰撞弹回沿斜面上升过程中,物块B的加速度a1大小是(k-1)gsinθ,方向沿斜面向上;
(2)从释放木板到木板与挡板第二次碰撞的瞬间,木板A运动的路程是
| (k+3)H |
| (k+1)sinθ |
(3)从释放木板到木板和物块都静止,木板和物块系统损失的机械能是
| 2kmgH |
| k-1 |
点评:此题考察到了能量的转化与守恒定律,牵扯到了重力和摩擦力做功,要注意的是重力做功与路径无关,至于初末位置的高度差有关;摩擦力做功会使机械能能转化为内能,等于在整个过程中机械能的损失.
在应用牛顿运动定律和运动学公式解决问题时,要注意运动过程的分析,此类问题,还要对整个运动进行分段处理.
在应用牛顿运动定律和运动学公式解决问题时,要注意运动过程的分析,此类问题,还要对整个运动进行分段处理.

练习册系列答案
相关题目

 ,斜面底端固定一个与斜面垂直的挡板,一木板A被在斜面上,其下端离地面高为H,上端放着一个小物块B,如图所示。木板和物块的质量均为m,相互间最大静摩擦力等于滑动摩擦力
,斜面底端固定一个与斜面垂直的挡板,一木板A被在斜面上,其下端离地面高为H,上端放着一个小物块B,如图所示。木板和物块的质量均为m,相互间最大静摩擦力等于滑动摩擦力 (A > 1),把它们由静止释放,木板与挡板发生碰撞时,时间极短,无动能损失,而物块不会与挡板发生碰撞.求:
(A > 1),把它们由静止释放,木板与挡板发生碰撞时,时间极短,无动能损失,而物块不会与挡板发生碰撞.求: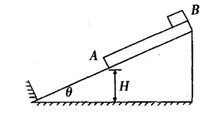
 ,斜面底端固定一个与斜面垂直的挡板,一木板A被在斜面上,其下端离地面高为H,上端放着一个小物块B,如图所示。木板和物块的质量均为m,相互间最大静摩擦力等于滑动摩擦力
,斜面底端固定一个与斜面垂直的挡板,一木板A被在斜面上,其下端离地面高为H,上端放着一个小物块B,如图所示。木板和物块的质量均为m,相互间最大静摩擦力等于滑动摩擦力 (A > 1),把它们由静止释放,木板与挡板发生碰撞时,时间极短,无动能损失,而物块不会与挡板发生碰撞.求:
(A > 1),把它们由静止释放,木板与挡板发生碰撞时,时间极短,无动能损失,而物块不会与挡板发生碰撞.求: