题目内容
如图所示，某人正通过定滑轮用不可伸长的轻质细绳将质量为m的货物提升到高处．已知人拉绳的端点沿平面向右运动，若滑轮的质量和摩擦均不计，则下列说法中正确的是（ ）分析：合运动与分运动的关系，在题中人的运动是合运动故将速度v沿绳分解，垂直于绳分解，根据几何关系找出分速度的变化，
根据牛顿第二定律求出绳的拉力T和物体的重力mg的关系．
根据牛顿第二定律求出绳的拉力T和物体的重力mg的关系．
解答：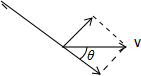
解：A、由题意可知，人的运动是合运动故将速度v沿绳分解，垂直与绳分解，如图示
沿绳的速度即货物提升的速度Vcosθ，θ随人向右运动变小，
人向右匀速运动时，V不变，所以Vcosθ变大，故货物做加速运动，
所以货物的加速度方向向上，由牛顿第二定律可知，
绳的拉力T大于物体的重力mg，故A错误，B正确．
C、人向右匀加速运动时，V随时间均匀增大，cosθ在增大，
所以物体做加速度增加的加速运动，故C正确，D错误．
故选BC．
解：A、由题意可知，人的运动是合运动故将速度v沿绳分解，垂直与绳分解，如图示沿绳的速度即货物提升的速度Vcosθ，θ随人向右运动变小，
人向右匀速运动时，V不变，所以Vcosθ变大，故货物做加速运动，
所以货物的加速度方向向上，由牛顿第二定律可知，
绳的拉力T大于物体的重力mg，故A错误，B正确．
C、人向右匀加速运动时，V随时间均匀增大，cosθ在增大，
所以物体做加速度增加的加速运动，故C正确，D错误．
故选BC．
点评：考查合运动即实际运动，将合运动速度v沿绳分解，垂直与绳分解，判断运动性质．
练习册系列答案
相关题目
（2009?江苏模拟）如图所示，某人正通过定滑轮将质量为m的货物提升到高处．滑轮的质量和摩擦均不计，货物获得的加速度a与绳子对货物竖直向上的拉力T之间的函数关系如图所示．以下判断正确的是（ ）
如图所示，某人正通过定滑轮将质量为m的货物提升到高处．滑轮的质量的摩擦均不计，货物获得的加速度a与绳子对货物竖直向上的拉力T之间的函数关系如图乙所示．由图象判断正确的是（ ）
