题目内容
【题目】一带正电荷的小球沿光滑、水平、绝缘的桌面向右运动，如图所示，速度方向垂直于一匀强磁场，飞离桌面后，最终落在地面上．设飞行时间为t1、水平射程为s1、着地速率为v1；现撤去磁场其它条件不变，小球飞行时间为t2、水平射程为s2、着地速率为v2 ． 则有（ ）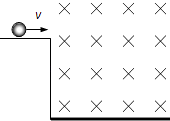
A.v1=v2
B.v1＞v2
C.s1=s2
D.t1＜t2
【答案】A
【解析】解：A、在有磁场，重力和洛仑兹力共同作用时，其洛仑兹力的方向每时每刻都跟速度方向垂直，不对粒子做功，不改变粒子的动能，有磁场和无磁场都只有重力作功，动能的增加是相同的．有磁场和无磁场，小球落地时速度方向并不相同，但速度的大小是相等的，即v1=v2，A符合题意，B不符合题意；
C、有磁场时，小球下落过程中要受重力和洛仑兹力共同作用，重力方向竖直向下，大小方向都不变；洛仑兹力的大小和方向都随速度的变化而变化，但在能落到地面的前提下洛仑兹力的方向跟速度方向垂直，总是指向右上方某个方向，其水平分力fx水平向右，竖直分力fy竖直向上．
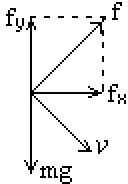
如图所示，竖直方向的加速度仍向下，但小于重力加速度g，从而使运动时间比撤去磁场后要长，即t1＞t2，小球水平方向也将加速运动，从而使水平距离比撤去磁场后要大，即s1＞s2，CD不符合题意；
所以答案是：A．
【考点精析】解答此题的关键在于理解匀变速直线运动的速度、位移、时间的关系的相关知识，掌握速度公式：V=V0+at；位移公式：s=v0t+1/2at2；速度位移公式：vt2-v02=2as；以上各式均为矢量式，应用时应规定正方向，然后把矢量化为代数量求解，通常选初速度方向为正方向，凡是跟正方向一致的取“+”值，跟正方向相反的取“-”值，以及对动能定理的综合应用的理解，了解应用动能定理只考虑初、末状态，没有守恒条件的限制，也不受力的性质和物理过程的变化的影响.所以，凡涉及力和位移，而不涉及力的作用时间的动力学问题，都可以用动能定理分析和解答，而且一般都比用牛顿运动定律和机械能守恒定律简捷．
