Question

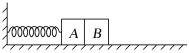
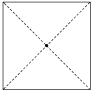
【题目】正方形木板水平放置在地面上，木板的中心静置一小滑块(可视为质点)，如图所示为俯视图，为将木板从滑块下抽出，需要对木板施加一个作用线通过木板中心点的水平恒力F.已知木板边长L＝2m、质量M＝3kg，滑块质量m＝2kg，滑块与木板、木板与地面间的动摩擦因数均为μ＝0.2，g取10m/s2，设最大静摩擦力等于滑动摩擦力.求：

(1)要将木板抽出，水平恒力F需满足的条件；

(2)当水平恒力F＝29N时，在木板抽出时滑块能获得的最大速率.

Answer 1

【答案】(1)F≥20N (2) m/s

【解析】(1)能抽出木板，滑块与木板发生相对滑动，当滑块达到随木板运动的最大加速度时，拉力最小.

对滑块，有：μmg＝ma

对木板，有：Fmin－μ(M＋m)g－μmg＝Ma

联立解得：Fmin＝2μ(M＋m)g＝20N

故抽出木板，水平恒力F至少为20N

(2)要使滑块获得的速度最大，则滑块在木板上相对滑动的距离最大，故应沿木板的对角线方向抽木板.

设此时木板加速度为a1，则有：

F－μ(M＋m)g－μmg＝Ma1

由：a1t2－μgt2＝L

vmax＝μgt

联立解得：

vmax＝m/s