题目内容
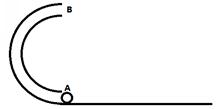
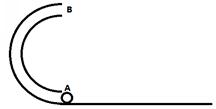
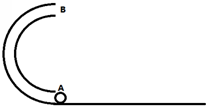
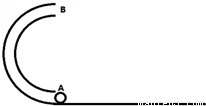
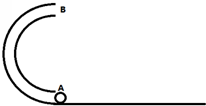 一内壁光滑的半环形细圆管竖直地固定在水平桌面上,其直径AB与桌面垂直,环的半径为R(比细管的半径大得多).一个质量为m的小球(小球直径略小于细管直径且可视为质点)从管口A射入管中,从管口B射出时对管口壁的压力为mg/3.求小球在桌面上的落点到管口A的距离.
一内壁光滑的半环形细圆管竖直地固定在水平桌面上,其直径AB与桌面垂直,环的半径为R(比细管的半径大得多).一个质量为m的小球(小球直径略小于细管直径且可视为质点)从管口A射入管中,从管口B射出时对管口壁的压力为mg/3.求小球在桌面上的落点到管口A的距离.分析:小球到达B处时,所受的弹力可能向上,也可能向下,由牛顿第二定律求得速度vB.小球离开B后做平抛运动,由高度求出时间,由水平方向匀速直线运动,由x=vBt求解小球在桌面上的落点到管口A的距离.
解答:解:当小球在B处所受弹力向上时,小球射出速度为v1,落点到A距离为x1.
由牛顿第二定律得 mg-
mg=m
得v1=
小球离开B后做平抛运动,则有
2R=
gt2
x1=v1t
解以上三个方程得:x1=2R
当小球在管口B处所受弹力向下时,小球射出速度为v2,落点到A的距离为x2.
mg+
mg=m
又2R=
gt2
x2=v2t
解以上三个方程得:x2=4R
答:小球在桌面上的落点到管口A的距离是2R
或4R
.
由牛顿第二定律得 mg-
| 1 |
| 3 |
| ||
| R |
得v1=
|
小球离开B后做平抛运动,则有
2R=
| 1 |
| 2 |
x1=v1t
解以上三个方程得:x1=2R
|
当小球在管口B处所受弹力向下时,小球射出速度为v2,落点到A的距离为x2.
mg+
| 1 |
| 3 |
| ||
| R |
又2R=
| 1 |
| 2 |
x2=v2t
解以上三个方程得:x2=4R
|
答:小球在桌面上的落点到管口A的距离是2R
|
|
点评:对于圆周运动,关键确定向心力的来源,要注意分析弹力可能的方向,不能漏解.对于平抛运动,运用运动的分解法研究.

练习册系列答案
相关题目