题目内容
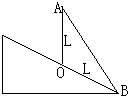
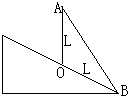
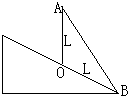如图所示，在离斜面底B点为L的O点竖直固定一长为L的直杆OA，A端与B点之间也用直杆连接．在杆上穿一光滑小环，先后两次从A点无初速度释放小环，第一次沿AO杆下滑，第二次沿AB杆下滑．重力加速度为g，则两次滑到斜面上所需的时间分别为t1=分析：根据牛顿第二定律求出加速度的大小，结合位移时间公式求出运动的时间．
解答：解：沿AO杆下滑，加速度a=g，位移为L，则L=
gt12，解得t1=
．
沿AB杆下滑，设∠OAB=α，则AB=2Lcosα，加速度a=
=gcosα．
根据2Lcosα=
gcosαt2，解得t2=2
．
故答案为：
，2
．
| 1 |
| 2 |
|
沿AB杆下滑，设∠OAB=α，则AB=2Lcosα，加速度a=
| mgcosα |
| m |
根据2Lcosα=
| 1 |
| 2 |
|
故答案为：
|
|
点评：解决本题的关键正确地受力分析，运用牛顿第二定律结合运动学公式进行求解，知道加速度是联系力学和运动学的桥梁．
练习册系列答案
相关题目
如图所示，在离斜面底B点为L的O点竖直固定一长为L的直杆OA，A端与B点之间也用直杆连接．在杆上穿一光滑小环，先后两次从A点无初速度释放小环，第一次沿AO杆下滑，第二次沿AB杆下滑．重力加速度为g，则两次滑到斜面上所需的时间分别为t1=________，t2=________．
