题目内容
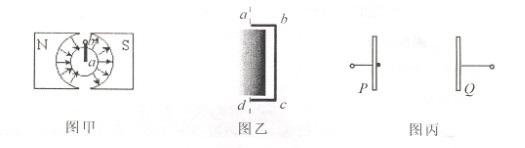
某种发电机的内部结构平面图如图甲,永磁体的内侧为半圆柱面形,它与圆柱形铁芯之间的窄缝间形成如图所示B=0.5T的磁场.在磁场中有一个如图乙所示的U形导线框abcd.已知线框ab和cd边长均为0.2m,bc边长为0.4m,线框以ω=200πrad/s角速度顺时针匀速转动.(1)从bc边转到图甲所示正上方开始计时,求t=2.5×10-3s这一时刻线框中感应电动势的大小,并在给定的坐标平面内画出ad两点电势差Uad随时间变化的关系图线.(感应电动势的结果保留两位有效数字,Uad正值表示Ua>Ud)
(2)如将此电压加在图丙所示的竖直放置的平行金属板上,且电动势为正时E板电势高,让一质量为m=6.4×10-13kg,电量为q=3.2×10-10C的带正电微粒从
 时刻开始由E板出发向F板运动,已知EF两板间距L=0.5m,粒子从E运动到F用多长时间?(粒子重力不计)
时刻开始由E板出发向F板运动,已知EF两板间距L=0.5m,粒子从E运动到F用多长时间?(粒子重力不计)

【答案】分析:(1)根据法拉第电磁感应定律E=BSω直接求出感应电动势的大小;通过右手定则确定ad两点间的电势高低,从而判断开始时ad间电势的高低,由图示电场知线框转过π弧度ag间电势将反向,根据已知的角速度可以求出电势变化的时间.
(2)抓住开始时的时间,在一个运动周期内:根据图象知,在t=6.00×10-3s时刻电动势为正的,粒子将向Y板做初速度为0的匀加速直线运动,运动时间为T-t然后再向Y板做匀减速直线运动,经过0.004s时速度减为0.然后再向X板匀加速0.001s,在紧接着的0.001s内粒子将向X板匀减速运动至速度为0,然后进入第二个运动周期.根据分段运动特点求出每个周期前进的距离,根据已知位移从而求出时间即可.
解答: 解:(1)线框转动过程中,bc边始终和磁场方向垂直,感应电动势大小不变,设t=2.5×10-3s的感应应电动势为E:
解:(1)线框转动过程中,bc边始终和磁场方向垂直,感应电动势大小不变,设t=2.5×10-3s的感应应电动势为E:
E=BL2?L1ω…①
带入数据得:E=25V…②
线框转动的周期: ,根据安培定则,从t=0开始,
,根据安培定则,从t=0开始, 内Uad为正值,
内Uad为正值, 内Uad为负值,图象如图,t=2.5×10-3s这一时刻线框转动
内Uad为负值,图象如图,t=2.5×10-3s这一时刻线框转动 ,所以线框中的感应电动势的大小为25V.
,所以线框中的感应电动势的大小为25V.
(2)在EF上加电压后,板间产生强度E不变,方向交替变化的匀强电场,微粒 时刻开始运动,运动情况如图,
时刻开始运动,运动情况如图, 设微粒在电场中运动的加速度为a,则有:
设微粒在电场中运动的加速度为a,则有:
 …③
…③
其中 …④
…④
 …⑤
…⑤
 …⑥
…⑥
微粒在一个周期内前进的距离S=2S1-2S1…⑦
由③④⑤⑥各式得:S=0.125m
由于粒子做往复运动,所以实际运动时间小于4T,设运动总时间为t,
t=3T+2×0.3T-△t…⑧
其中△t满足: …⑨
…⑨
由以上各式t=3.32×10-2s…⑩
答:(1)t=2.5×10-3s这一时刻线框中感应电动势的大小为25V,ad两点电势差Uad随时间变化的关系图线如图.
(2)粒子从E运动到F用的时间为3.32×10-2s.
点评:掌握法拉第电磁感应定律及通过右手定则判断感应电势的高低是解决本题前两问的基础,在粒子往复运动中根据粒子的受力特点和运动的周期性展开讨论即可.
(2)抓住开始时的时间,在一个运动周期内:根据图象知,在t=6.00×10-3s时刻电动势为正的,粒子将向Y板做初速度为0的匀加速直线运动,运动时间为T-t然后再向Y板做匀减速直线运动,经过0.004s时速度减为0.然后再向X板匀加速0.001s,在紧接着的0.001s内粒子将向X板匀减速运动至速度为0,然后进入第二个运动周期.根据分段运动特点求出每个周期前进的距离,根据已知位移从而求出时间即可.
解答:
 解:(1)线框转动过程中,bc边始终和磁场方向垂直,感应电动势大小不变,设t=2.5×10-3s的感应应电动势为E:
解:(1)线框转动过程中,bc边始终和磁场方向垂直,感应电动势大小不变,设t=2.5×10-3s的感应应电动势为E:E=BL2?L1ω…①
带入数据得:E=25V…②
线框转动的周期:
 ,根据安培定则,从t=0开始,
,根据安培定则,从t=0开始, 内Uad为正值,
内Uad为正值, 内Uad为负值,图象如图,t=2.5×10-3s这一时刻线框转动
内Uad为负值,图象如图,t=2.5×10-3s这一时刻线框转动 ,所以线框中的感应电动势的大小为25V.
,所以线框中的感应电动势的大小为25V.(2)在EF上加电压后,板间产生强度E不变,方向交替变化的匀强电场,微粒
 时刻开始运动,运动情况如图,
时刻开始运动,运动情况如图, 设微粒在电场中运动的加速度为a,则有:
设微粒在电场中运动的加速度为a,则有: …③
…③其中
 …④
…④ …⑤
…⑤ …⑥
…⑥微粒在一个周期内前进的距离S=2S1-2S1…⑦
由③④⑤⑥各式得:S=0.125m
由于粒子做往复运动,所以实际运动时间小于4T,设运动总时间为t,
t=3T+2×0.3T-△t…⑧
其中△t满足:
 …⑨
…⑨由以上各式t=3.32×10-2s…⑩
答:(1)t=2.5×10-3s这一时刻线框中感应电动势的大小为25V,ad两点电势差Uad随时间变化的关系图线如图.
(2)粒子从E运动到F用的时间为3.32×10-2s.
点评:掌握法拉第电磁感应定律及通过右手定则判断感应电势的高低是解决本题前两问的基础,在粒子往复运动中根据粒子的受力特点和运动的周期性展开讨论即可.

练习册系列答案
相关题目
某种发电机的内部结构平面图如图甲,永磁体的内侧为半圆柱面形,它与圆柱形铁芯之间的窄缝间形成如图所示B=0.5T的磁场.在磁场中有一个如图乙所示的U形导线框abcd.已知线框ab和cd边长均为0.2m,bc边长为0.4m,线框以ω=200πrad/s角速度顺时针匀速转动.

 |
(1)从bc边转到图甲所示正上方开始计时,求t=2.5×10-3s这一时刻线框中感应电动势的大小,并在给定的坐标平面内画出ad两点电势差Uad随时间变化的关系图线.(感应电动势的结果保留两位有效数字,Uad正值表示Ua>Ud)
(2)如将此电压加在图丙所示的竖直放置的平行金属板上,且电动势为正时E板电势高,让一质量为m=6.4×10-13kg,电量为q=3.2×10-10C的带正电微粒从![]() 时刻开始由E板出发向F板运动,已知EF两板间距L=0.5m,粒子从E运动到F用多长时间?(粒子重力不计)
时刻开始由E板出发向F板运动,已知EF两板间距L=0.5m,粒子从E运动到F用多长时间?(粒子重力不计)
某种发电机的内部结构平面图如图甲,永磁体的内侧为半圆柱面形,它与圆柱形铁芯之间的窄缝间形成如图所示B=0.5T的磁场.在磁场中有一个如图乙所示的U形导线框abcd.已知线框ab和cd边长均为0.2m,bc边长为0.4m,线框以ω=200πrad/s角速度顺时针匀速转动.
(1)从bc边转到图甲所示正上方开始计时,求t=2.5×10-3s这一时刻线框中感应电动势的大小,并在给定的坐标平面内画出ad两点电势差Uad随时间变化的关系图线.(感应电动势的结果保留两位有效数字,Uad正值表示Ua>Ud)(2)如将此电压加在图丙所示的竖直放置的平行金属板上,且电动势为正时E板电势高,让一质量为m=6.4×10-13kg,电量为q=3.2×10-10C的带正电微粒从 时刻开始由E板出发向F板运动,已知EF两板间距L=0.5m,粒子从E运动到F用多长时间?(粒子重力不计)
时刻开始由E板出发向F板运动,已知EF两板间距L=0.5m,粒子从E运动到F用多长时间?(粒子重力不计)

 |
(1)从bc边转到图甲所示正上方开始计时,求t=2.5×10-3s这一时刻线框中感应电动势的大小,并在给定的坐标平面内画出ad两点电势差Uad随时间变化的关系图线.(感应电动势的结果保留两位有效数字,Uad正值表示Ua>Ud)(2)如将此电压加在图丙所示的竖直放置的平行金属板上,且电动势为正时E板电势高,让一质量为m=6.4×10-13kg,电量为q=3.2×10-10C的带正电微粒从
 某种发电机的内部结构平面图如图甲,永磁体的内侧为半圆柱面形,它与圆柱形铁芯之间的窄缝间形成如图所示B=0.5T的磁场.在磁场中有一个如图乙所示的U形导线框abcd.已知线框ab和cd边长均为0.2m,bc边长为0.4m,线框以ω=200πrad/s角速度顺时针匀速转动.
某种发电机的内部结构平面图如图甲,永磁体的内侧为半圆柱面形,它与圆柱形铁芯之间的窄缝间形成如图所示B=0.5T的磁场.在磁场中有一个如图乙所示的U形导线框abcd.已知线框ab和cd边长均为0.2m,bc边长为0.4m,线框以ω=200πrad/s角速度顺时针匀速转动. 求t=2.5×10-3s这一时刻线框中感应电动势的大小,并在给定的坐标平面内画出ad两点电势差Uad随时间变化的关系图线.(感应电动势的结果保留两位有效数字,Uad正值表示Ua>Ud)
求t=2.5×10-3s这一时刻线框中感应电动势的大小,并在给定的坐标平面内画出ad两点电势差Uad随时间变化的关系图线.(感应电动势的结果保留两位有效数字,Uad正值表示Ua>Ud)