题目内容
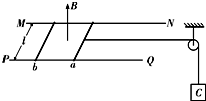 如图所示,间距为l、电阻不计的两根平行金属导轨MN、PQ(足够长)被固定在同一水平面内,质量均为m、电阻均为R的两根相同导体棒a、b垂直于导轨放在导轨上,一根轻绳绕过定滑轮后沿两金属导轨的中线与a棒连接,其下端悬挂一个质量为M的物体C,整个装置放在方向竖直向上、磁感应强度大小为B的匀强磁场中.开始时使a、b、C都处于静止状态,现释放C,经过时间t,C的速度为v1、b的速度为v2,不计一切摩擦,两棒始终与导轨接触良好,重力加速度为g,求:
如图所示,间距为l、电阻不计的两根平行金属导轨MN、PQ(足够长)被固定在同一水平面内,质量均为m、电阻均为R的两根相同导体棒a、b垂直于导轨放在导轨上,一根轻绳绕过定滑轮后沿两金属导轨的中线与a棒连接,其下端悬挂一个质量为M的物体C,整个装置放在方向竖直向上、磁感应强度大小为B的匀强磁场中.开始时使a、b、C都处于静止状态,现释放C,经过时间t,C的速度为v1、b的速度为v2,不计一切摩擦,两棒始终与导轨接触良好,重力加速度为g,求:(1)t时刻C的加速度值;
(2)t时刻a、b与导轨所组成的闭合回路消耗的热功率;
(3)t时刻a、b与导轨所组成的闭合回路消耗的总电功率.
分析:(1)由F=BIL求出棒a、b所受的安培力大小,根据牛顿第二定律分别研究棒ab和A物体,可求解加速度.
(2)(2)t时刻a、b与导轨所组成的闭合回路消耗的热功率为.
(3)单位时间内,通过a棒克服安培力做功,把C物体的一部分重力势能转化为闭合回路的电能,而闭合回路电能的一部分以焦耳热的形式消耗掉,另一部分则转化为b棒的动能.
(2)(2)t时刻a、b与导轨所组成的闭合回路消耗的热功率为.
(3)单位时间内,通过a棒克服安培力做功,把C物体的一部分重力势能转化为闭合回路的电能,而闭合回路电能的一部分以焦耳热的形式消耗掉,另一部分则转化为b棒的动能.
解答:解:(1)根据法拉第电磁感应定律,t时刻回路的感应电动势为
E=
=Bl(v1-v2)
回路中感应电流 I=
根据牛顿第二定律:
对a有 T-BIl=ma
对C有 Mg-T=Ma
联立以上各式解得 a=
(2)t时刻a、b与导轨所组成的闭合回路消耗的热功率为
P1=I2?2R=
(3)单位时间内,通过a棒克服安培力做功,把C物体的一部分重力势能转化为闭合回路的电能,而闭合回路电能的一部分以焦耳热的形式消耗掉,另一部分则转化为b棒的动能,所以,t时刻闭合回路的电功率等于a棒克服安培力做功的功率,即
P总=BIl?v1=
答:(1)t时刻C的加速度值a=
;
(2)t时刻a、b与导轨所组成的闭合回路消耗的热功率P1=
;
(3)t时刻a、b与导轨所组成的闭合回路消耗的总电功率
.
E=
| △Φ |
| △t |
回路中感应电流 I=
| E |
| 2R |
根据牛顿第二定律:
对a有 T-BIl=ma
对C有 Mg-T=Ma
联立以上各式解得 a=
| 2MgR-B2l2(v1-v2) |
| 2R(M+m) |
(2)t时刻a、b与导轨所组成的闭合回路消耗的热功率为
P1=I2?2R=
| B2l2(v1-v2)2 |
| 2R |
(3)单位时间内,通过a棒克服安培力做功,把C物体的一部分重力势能转化为闭合回路的电能,而闭合回路电能的一部分以焦耳热的形式消耗掉,另一部分则转化为b棒的动能,所以,t时刻闭合回路的电功率等于a棒克服安培力做功的功率,即
P总=BIl?v1=
| B2l2(v1-v2)?v1 |
| 2R |
答:(1)t时刻C的加速度值a=
| 2MgR-B2l2(v1-v2) |
| 2R(M+m) |
(2)t时刻a、b与导轨所组成的闭合回路消耗的热功率P1=
| B2l2(v1-v2)2 |
| 2R |
(3)t时刻a、b与导轨所组成的闭合回路消耗的总电功率
| B2l2(v1-v2)?v1 |
| 2R |
点评:本题综合考查了法拉第电磁感应定律以及电磁感应中的能量守恒.关键理清导体棒的运动情况,选择合适的定律进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,间距为L的两根长直平行导轨M、N所在平面与水平面夹角为θ,磁感应强度为B的匀强磁场垂直轨道平面.横跨的导体棒cd因为摩擦而处于静止状态,其质量为M.另一根导体棒ab质量为m,由静止开始沿轨道无摩擦由上方滑下,当沿轨道下滑距离为S时,达到最大速度.在ab下滑过程中,cd棒始终保持静止.两棒电阻均为R,导轨电阻不计.求:
如图所示,间距为L的两根长直平行导轨M、N所在平面与水平面夹角为θ,磁感应强度为B的匀强磁场垂直轨道平面.横跨的导体棒cd因为摩擦而处于静止状态,其质量为M.另一根导体棒ab质量为m,由静止开始沿轨道无摩擦由上方滑下,当沿轨道下滑距离为S时,达到最大速度.在ab下滑过程中,cd棒始终保持静止.两棒电阻均为R,导轨电阻不计.求: 如图所示,间距为L、半径为R0的内壁光滑的
如图所示,间距为L、半径为R0的内壁光滑的 (2009?广州三模)如图所示,间距为L,电阻不计的两根平行金属导轨MN、PQ(足够长)被固定在同一水平面内,质量均为m,电阻均为R的两根相同导体棒a、b垂直于导轨放在导轨上,一根轻绳绕过定滑轮后沿两金属导轨的中线与a棒连连,其下端悬挂一个质量为M的物体C,整个装置放在方向竖直向上,磁感应强度大小为B的匀强磁场中,开始时使a、b、C都处于静止状态,现释放C,经过时间t,C的速度为v1,b的速度为v2.不计一切摩擦,两棒始终与导轨接触良好,重力加速度为g,求:
(2009?广州三模)如图所示,间距为L,电阻不计的两根平行金属导轨MN、PQ(足够长)被固定在同一水平面内,质量均为m,电阻均为R的两根相同导体棒a、b垂直于导轨放在导轨上,一根轻绳绕过定滑轮后沿两金属导轨的中线与a棒连连,其下端悬挂一个质量为M的物体C,整个装置放在方向竖直向上,磁感应强度大小为B的匀强磁场中,开始时使a、b、C都处于静止状态,现释放C,经过时间t,C的速度为v1,b的速度为v2.不计一切摩擦,两棒始终与导轨接触良好,重力加速度为g,求: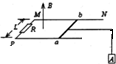 如图所示,间距为L、电阻不计的两根平行金属导轨MN、PQ(足够长)被固定在同一水平面内,M、P间连接了一电阻R长度为L、质量为m、电阻也为R的导体棒ab垂直置于导轨上,一根轻绳绕过定滑轮后沿两金属导轨的中线与ab棒连接,其下端悬挂一个质量也为m的物体A,整个装置处于方向竖直向上、磁感应强度大小为B的匀强磁场中.开始时使导体棒ab和物体A都处于静止状态且轻绳拉直,现释放A,经过时间t,物体A下降的高度为h,速度为v.不计一切摩擦,导体棒始终与导轨接触良好,重力加速度为g.
如图所示,间距为L、电阻不计的两根平行金属导轨MN、PQ(足够长)被固定在同一水平面内,M、P间连接了一电阻R长度为L、质量为m、电阻也为R的导体棒ab垂直置于导轨上,一根轻绳绕过定滑轮后沿两金属导轨的中线与ab棒连接,其下端悬挂一个质量也为m的物体A,整个装置处于方向竖直向上、磁感应强度大小为B的匀强磁场中.开始时使导体棒ab和物体A都处于静止状态且轻绳拉直,现释放A,经过时间t,物体A下降的高度为h,速度为v.不计一切摩擦,导体棒始终与导轨接触良好,重力加速度为g.