题目内容
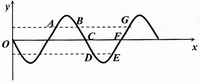
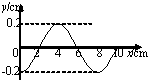
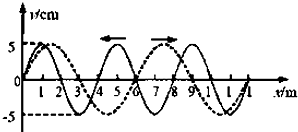
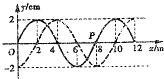
一列简谐横波在x轴上传播,在t1=0和t2=0.05s时,其波形图分别用如图所示的实线和虚线表示,求:
①这列波可能具有的波速.
②当波速为280m/s时,波的传播方向如何?以此波速传播时,x=8m处的质点P从平衡位置运动至波谷所需的最短时间是多少?
①这列波可能具有的波速.
②当波速为280m/s时,波的传播方向如何?以此波速传播时,x=8m处的质点P从平衡位置运动至波谷所需的最短时间是多少?

(1)由对波形图分析可知,该波波长λ=8m.若波沿x轴正向传播,则有:
△x1=nλ+
=(8n+2)=v1△t(n=0、1、2、3…)
所以:v1=(8n+2)
=(8n+2)×
=(40+160n)m/s
若波沿x轴负向传播,则有:
△x2=nλ+
=(8n+6)=v2△t(n=0、1、2、3…)
所以:v2=(8n+6)
=(8n+6)×
=(120+160n)m/s
于是得到波速v的通式为:v=(40+80k)m/s
当k=0、2、4…时,波沿x轴正向传播.
当k=1、3、5…时,波沿x轴负向传播.
(2)当波速为280m/s时,则有:280=40+80k.
解得:k=3故波沿-x方向传播.
因为:v=
所以:T=
=
s=
s
P质点第一次达到波谷的所历时间为:
t=
T=
×
=
=2.1×10-2s
答:(1)这列波可能具有的波速v=(40+80k)m/s
当k=0、2、4…时,波沿x轴正向传播.
当k=1、3、5…时,波沿x轴负向传播.
(2)当波速为280m/s时,波沿-x方向传播.此时图中质点P从图中位置运动至波谷所需的最短时间是2.1×10-2s.
△x1=nλ+
| λ |
| 4 |
所以:v1=(8n+2)
| 1 |
| △t |
| 1 |
| 0.05 |
若波沿x轴负向传播,则有:
△x2=nλ+
| 3λ |
| 4 |
所以:v2=(8n+6)
| 1 |
| △t |
| 1 |
| 0.05 |
于是得到波速v的通式为:v=(40+80k)m/s
当k=0、2、4…时,波沿x轴正向传播.
当k=1、3、5…时,波沿x轴负向传播.
(2)当波速为280m/s时,则有:280=40+80k.
解得:k=3故波沿-x方向传播.
因为:v=
| λ |
| T |
所以:T=
| λ |
| v |
| 8 |
| 280 |
| 1 |
| 35 |
P质点第一次达到波谷的所历时间为:
t=
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 35 |
| 3 |
| 140 |
答:(1)这列波可能具有的波速v=(40+80k)m/s
当k=0、2、4…时,波沿x轴正向传播.
当k=1、3、5…时,波沿x轴负向传播.
(2)当波速为280m/s时,波沿-x方向传播.此时图中质点P从图中位置运动至波谷所需的最短时间是2.1×10-2s.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目