Question

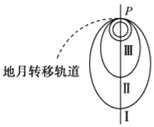
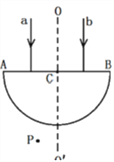
【题目】（14分）如图所示，轮半径r＝10 cm的传送带，水平部分AB的长度L＝1.5 m，与一圆心在O点、半径R＝1 m的竖直光滑圆轨道的末端相切于A点，AB高出水平地面H＝1.25 m，一质量m＝0.1 kg的小滑块(可视为质点)，由圆轨道上的P点从静止释放，OP与竖直线的夹角θ＝37°.已知sin 37°＝0.6，cos 37°＝0.8，g＝10 m/s2，滑块与传送带间的动摩擦因数μ＝0.1，不计空气阻力．

(1)求滑块对圆轨道末端的压力；

(2)若传送带一直保持静止，求滑块的落地点与B间的水平距离；

(3)若传送带以v0＝0.5 m/s的速度沿逆时针方向运行(传送带上部分由B到A运动)，求滑块在传送带上滑行过程中产生的内能．

Answer 1

【答案】（1） 1.4 N （2）0.5 m （3）0.2 J

【解析】

试题分析：(1)从P点到圆轨道末端的过程中，由机械能守恒定律得：mgR(1－cos 37°)＝mv2

在轨道末端由牛顿第二定律得： FN－mg＝,由以上两式得FN＝1.4 N，由牛顿第三定律得，滑块对圆轨道末端的压力大小为1.4 N，方向竖直向下。

(2)若传送带静止，从A到B的过程中，由动能定理得：－μmgL＝m－mv2

解得：vB＝1 m/s ；

滑块从B点开始做平抛运动，滑块的落地点与B点间的水平距离为： x＝vB＝0.5 m.

(3)传送带向左运动和传送带静止时，滑块的受力情况没有变化，滑块从A到B的运动情况没有改变．所以滑块和传送带间的相对位移为：Δx＝L＋v0＝2 m

滑块在传送带上滑行过程中产生的内能为： Q＝μmgΔx＝0.2 J.