题目内容
3. 在图示的电路中,电阻R1=100Ω,R2=200Ω,R3=50Ω,电源的电动势为12V,内阻不计,若电容器电容C=20μF,带电量为4×10-5C,当电键断开时,通过电阻R1的电量为多少?
在图示的电路中,电阻R1=100Ω,R2=200Ω,R3=50Ω,电源的电动势为12V,内阻不计,若电容器电容C=20μF,带电量为4×10-5C,当电键断开时,通过电阻R1的电量为多少?
分析 根据电容器的电荷量和电容求出电容器两端的电势差,结合串并联电路的特点,结合欧姆定律求出R4的阻值,断开电键后,结合电流分布求出通过电阻R1的电量.
解答 解:电容器两端间的电势差U=$\frac{Q}{C}=\frac{4×1{0}^{-5}}{20×1{0}^{-6}}=2V$,
设电源负极电势为0,则a点与负极的电势差${U}_{ao}=\frac{12}{100+200}×200V=8V$,即a点电势为8V,
若a点的电势比b点电势高2V,则b点电势为6V,
解得${R}_{4}=\frac{{U}_{4}}{I}=\frac{6}{\frac{12-6}{50}}Ω=50Ω$,
因为$\frac{{R}_{1}+{R}_{3}}{{R}_{2}+{R}_{4}}=\frac{150}{250}=\frac{3}{5}$,可知断开电键后,通过电阻R1的电量${Q}_{1}=\frac{5}{3+5}Q=\frac{5}{8}×4×1{0}^{-5}C$=2.5×10-5C.
若a但电势比b点电势低2C,则b点电势为10V,
解得${R}_{4}=\frac{{U}_{4}}{I}=\frac{10}{\frac{12-10}{50}}Ω=250Ω$,
因为$\frac{{R}_{1}+{R}_{3}}{{R}_{2}+{R}_{4}}=\frac{150}{450}=\frac{1}{3}$,可知断开电键后,通过电阻R1的电量${Q}_{1}′=\frac{3}{4}Q=\frac{3}{4}×4×1{0}^{-5}C$=3×10-5C.
答:通过电阻R1的电量为2.5×10-5C或3×10-5C.
点评 解决本题的关键知道电容器电势差和电荷量的关系,结合串并联电路的特点进行求解,注意a点的电势比b点电势可能高,可能低.

 英才计划期末调研系列答案
英才计划期末调研系列答案| A. | 1 N | B. | 2 N | C. | 5 N | D. | 7 N |
 如图所示,虚线a、b、c代表电场中三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )
如图所示,虚线a、b、c代表电场中三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )| A. | 三个等势面中,a的电势最低 | |
| B. | 三个等势面中,c的电势最低 | |
| C. | 带电质点通过P点时的速度比通过Q点时大 | |
| D. | 带电质点通过P点时的加速度比通过Q点时大 |
| A. | 物体的重力势能减少$\frac{mgh}{3}$ | B. | 物体的机械能减少$\frac{2mgh}{3}$ | ||
| C. | 物体的动能增加$\frac{2mgh}{3}$ | D. | 电场力对物体做功$\frac{2mgh}{3}$ |
| A. | 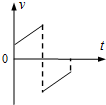 | B. |  | C. |  | D. |  |
(1)(单选)在研究物体的“加速度、作用力和质量”三个物理量的关系时,我们用实验研究了小车“在质量一定的情况下,加速度和作用力的关系”;又研究了“在作用力一定的情况下,加速度和质量之间的关系”.这种研究物理问题的科学方法是B
A.建立理想模型的方法 B.控制变量法C.等效替代法 D.类比法
(2)(单选)研究作用力一定时加速度与质量成反比的结论时,下列说法中正确的是D
A.平衡摩擦力时,应将装砂的小桶用细绳通过定滑轮系在小车上
B.每次改变小车质量时,要重新平衡摩擦力
C.实验时,先放开小车,再接通打点计时器的电源
D.在小车中增减砝码,应使小车和砝码的质量远大于砂和小桶的总质量
(3)某次实验中得到一条纸带,如图1所示,从比较清晰的点起,每5个计时点取一个计数点,分别标明0、1、2、3、4…,量得0与 1两点间距离x1=30mm,1与2两点间距离x2=36mm,2与3两点间距离x3=42mm,3与4两点间的距离x4=48mm,则小车在打计数点2时的瞬时速度为0.39 m/s,小车的加速度为0.6m/s2.

(4)某同学测得小车的加速度a和拉力F的数据如表所示:(小车质量保持不变)
| F/N | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
| a/m•s-2 | 0.10 | 0.20 | 0.28 | 0.40 | 0.52 |
②图线不过原点的原因可能是没有平衡摩擦力或平衡摩擦力不够.
③图中的力F理论上指B,而实验中却用A表示.(选填字母符号)
A.砂和砂桶的重力 B.绳对小车的拉力.
 如图所示,为一交流电发电机构造示意图,矩形线圈abcd,已知ad=L1,ab=L2,匝数为n,线圈绕OO′轴在磁感应强度为B的匀强磁场中以角速度ω匀速转动,线圈电阻为r,外电路电阻为R,求:
如图所示,为一交流电发电机构造示意图,矩形线圈abcd,已知ad=L1,ab=L2,匝数为n,线圈绕OO′轴在磁感应强度为B的匀强磁场中以角速度ω匀速转动,线圈电阻为r,外电路电阻为R,求: