��Ŀ����
8��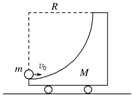 ����ΪM��С����ֹ�ڹ⻬ˮƽ���ϣ�������һ���ķ�֮һԲ�ܵĹ⻬���������¶�����ˮƽ������Ϊm��С����ˮƽ����ӹ���¶��Գ��ٶ�v0����С�����������ٶ�Ϊg����ͼ��ʾ����֪С��С���϶��뿪С����С����С���ֻ��£���С������ʱ��С����С���ٶȷ����෴���ٶȴ�С֮�ȵ���1��3����m��M��ֵΪ��������
����ΪM��С����ֹ�ڹ⻬ˮƽ���ϣ�������һ���ķ�֮һԲ�ܵĹ⻬���������¶�����ˮƽ������Ϊm��С����ˮƽ����ӹ���¶��Գ��ٶ�v0����С�����������ٶ�Ϊg����ͼ��ʾ����֪С��С���϶��뿪С����С����С���ֻ��£���С������ʱ��С����С���ٶȷ����෴���ٶȴ�С֮�ȵ���1��3����m��M��ֵΪ��������| A�� | 1��3 | B�� | 3��1 | C�� | 3��5 | D�� | 5��3 |
���� ϵͳ��ˮƽ�������غ㣬�ɶ����غ㶨����ʽ��ͬʱϵͳ��е���غ㣬���ɻ�е���غ���ʽ��⣬������֪�������������֮�ȣ�
��� �⣺��С��ij��ٶȷ���Ϊ�������ɶ����غ��֪��
mv0=Mv1-mv2
$\frac{{v}_{1}}{{v}_{2}}$=$\frac{3}{1}$
�������л�е���غ㶨�ɿɵã�
$\frac{1}{2}$mv02=$\frac{1}{2}$Mv12+$\frac{1}{2}$mv22
������ã�$\frac{m}{M}$=$\frac{3}{5}$
��ѡ��C��
���� ���⿼�鶯���غ㼰��е���غ��Ӧ�ã�Ҫע��������غ㶨�ɵ�������ֻҪ���������������غ���ʽ��⣮

��ϰ��ϵ�д�
 ������ϰ�ο����뵥Ԫ���ϵ�д�
������ϰ�ο����뵥Ԫ���ϵ�д� �����Ծ���ĩ���100��ϵ�д�
�����Ծ���ĩ���100��ϵ�д�
�����Ŀ
20�����й�IJ��������Ե�˵���У���ȷ���ǣ�������
| A�� | �еĹ��Dz����еĹ������� | |
| B�� | �����������ͬ����һ������ | |
| C�� | ��IJ���Խ�����䲨����Խ����������Խ�̣���������Խ���� | |
| D�� | �������ӵ���Ϊ������ʾ�������� |
17�����ڵ�ų��͵�Ų�����ȷ˵���ǣ�������
| A�� | �糡�ʹų��������ϵ�ģ�����ͳ��Ϊ��ų� | |
| B�� | ��ų��ɷ�����������Զ���Ĵ����γɵ�Ų� | |
| C�� | �ڵ糡��Χһ�������ų����ų���Χһ�������糡 | |
| D�� | ��Ų���һ�����ʣ�����������д��� |
18�� λ������ԭ��IJ�Դ����һ����x���������IJ�������Ϊ20m/s����֪t=0ʱ�����պô�����x=40m������ͼ��ʾ�������x=400m������һ��������������˵������ȷ���ǣ�������
λ������ԭ��IJ�Դ����һ����x���������IJ�������Ϊ20m/s����֪t=0ʱ�����պô�����x=40m������ͼ��ʾ�������x=400m������һ��������������˵������ȷ���ǣ�������
 λ������ԭ��IJ�Դ����һ����x���������IJ�������Ϊ20m/s����֪t=0ʱ�����պô�����x=40m������ͼ��ʾ�������x=400m������һ��������������˵������ȷ���ǣ�������
λ������ԭ��IJ�Դ����һ����x���������IJ�������Ϊ20m/s����֪t=0ʱ�����պô�����x=40m������ͼ��ʾ�������x=400m������һ��������������˵������ȷ���ǣ�������| A�� | ��Դ������������ | |
| B�� | x=40 m���ʵ���t=0.5 sʱλ��Ϊ��� | |
| C�� | ������t=1 sʱ���ܽ��յ��˲� | |
| D�� | ����Դ��x�Ḻ�����ƶ�������������յ��IJ���Ƶ�ʽ����� |
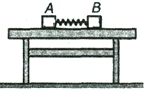 ��֤�������غ�ʵ�顷�У���ͬѧ�������ͼ��ʾ��װ�ý�����֤��������£�
��֤�������غ�ʵ�顷�У���ͬѧ�������ͼ��ʾ��װ�ý�����֤��������£�
 ��ͼ��ʾ������Ϊ1kg��С���ó�Ϊ0.5m��ϸ��������O�㣬O������߶�Ϊ5.4m�����ʹС����OO������ˮƽ������Բ���˶�����ϸ���ܵ�����Ϊ12.5Nʱ�ͻ����ϣ���
��ͼ��ʾ������Ϊ1kg��С���ó�Ϊ0.5m��ϸ��������O�㣬O������߶�Ϊ5.4m�����ʹС����OO������ˮƽ������Բ���˶�����ϸ���ܵ�����Ϊ12.5Nʱ�ͻ����ϣ���