题目内容
 如图所示,bc为固定在车上的水平横杆,物块M串在杆上,靠摩擦力保持相对杆静止,M又通过经细线悬吊着一个小铁球m,此时小车正以大小为a的加速度向右做匀加速直线运动,而M、m均相对小车静止,细线与竖直方向的夹角为θ,小车的加速度逐渐增大,M始终和小车相对静止,当加速度增加到2a时( )
如图所示,bc为固定在车上的水平横杆,物块M串在杆上,靠摩擦力保持相对杆静止,M又通过经细线悬吊着一个小铁球m,此时小车正以大小为a的加速度向右做匀加速直线运动,而M、m均相对小车静止,细线与竖直方向的夹角为θ,小车的加速度逐渐增大,M始终和小车相对静止,当加速度增加到2a时( )分析:先对小球受力分析,根据牛顿第二定律列式分析;再对小球和滑块整体受力分析,根据牛顿第二定律列式求解.
解答:解:对小球受力分析,受重力mg和细线的拉力T,如图
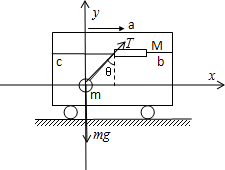
根据牛顿第二定律,有
Tsinθ=ma ①
Tcosθ-mg=0 ②
再对m和M整体受力分析,受总重力(M+m)g、支持力N、摩擦力f,如图

根据牛顿第二定律,有
f=(M+m)a ③
N-(M+m)g=0 ④
由①②③④解得:
tanθ=
N=(M+m)g
T=
f=(M+m)a
当加速度变为2倍时,摩擦力f变为2倍,故A正确;
支持力N不变,故B正确;
θ的正切变为原来的2倍,但θ不是2倍,故C错误;
由于T=
,故T不是增加原来的2倍,故D错误;
故选AB.

根据牛顿第二定律,有
Tsinθ=ma ①
Tcosθ-mg=0 ②
再对m和M整体受力分析,受总重力(M+m)g、支持力N、摩擦力f,如图

根据牛顿第二定律,有
f=(M+m)a ③
N-(M+m)g=0 ④
由①②③④解得:
tanθ=
| a |
| g |
N=(M+m)g
T=
| m(a2+g2) |
f=(M+m)a
当加速度变为2倍时,摩擦力f变为2倍,故A正确;
支持力N不变,故B正确;
θ的正切变为原来的2倍,但θ不是2倍,故C错误;
由于T=
| m(a2+g2) |
故选AB.
点评:本题关键是先后对小球、滑块与小球整体受力分析后根据牛顿第二定律列式求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,bc为固定在车上的水平横杆,物块M串在杆上,靠摩擦力保持相对杆静止,M又通过细线悬吊着一个小铁球m,此时小车正以大小为a的加速度向右做匀加速直线运动,而M、m均相对小车静止,细线与竖直方向的夹角为θ,小车的加速度逐渐增大,M始终和小车保持相对静止,当加速度增加到2a时( )
如图所示,bc为固定在车上的水平横杆,物块M串在杆上,靠摩擦力保持相对杆静止,M又通过细线悬吊着一个小铁球m,此时小车正以大小为a的加速度向右做匀加速直线运动,而M、m均相对小车静止,细线与竖直方向的夹角为θ,小车的加速度逐渐增大,M始终和小车保持相对静止,当加速度增加到2a时( )| A、细线与竖直方向的夹角的正切值增加到原来的2倍 | B、横杆对M的摩擦力增加了Ma | C、横杆对M弹力不变 | D、细线的拉力小于原来的2倍 |
 如图所示,bc为固定在车上的水平横杆,物块M套在杆上,靠摩擦力保持相对杆静止,M又通过轻弹簧悬吊着一个小铁球m,此时小车正以大小为a的加速度向右做匀加速直线运动,而M、m均相对小车静止,轻弹簧与竖直方向的夹角为θ.小车的加速度逐渐增大,M始终和小车保持相对静止,当加速度增加到2a时( )
如图所示,bc为固定在车上的水平横杆,物块M套在杆上,靠摩擦力保持相对杆静止,M又通过轻弹簧悬吊着一个小铁球m,此时小车正以大小为a的加速度向右做匀加速直线运动,而M、m均相对小车静止,轻弹簧与竖直方向的夹角为θ.小车的加速度逐渐增大,M始终和小车保持相对静止,当加速度增加到2a时( )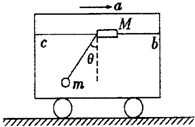 如图所示,bc为固定在小车上的水平横杆,物块M串在杆上,靠摩擦力保持相对杆静止,M又通过轻细线悬吊着一个小铁球m,此时小车正以大小为a的加速度向右做匀加速运动,而M、m均相对小车静止,细线与竖直方向的夹角为θ.小车的加速度逐渐增大,M始终和小车保持相对静止,当加速度增加到2a时( )
如图所示,bc为固定在小车上的水平横杆,物块M串在杆上,靠摩擦力保持相对杆静止,M又通过轻细线悬吊着一个小铁球m,此时小车正以大小为a的加速度向右做匀加速运动,而M、m均相对小车静止,细线与竖直方向的夹角为θ.小车的加速度逐渐增大,M始终和小车保持相对静止,当加速度增加到2a时( )