题目内容
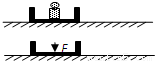
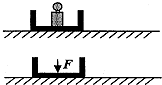 如图所示,木盒中固定一质量为m的砝码,木盒和砝码在桌面上一起以初速度v0滑行一段距离s1后停止.今拿走砝码,而持续加一个竖直向下的恒力F(F=mg),其他条件不变,木盒滑行的距离s2,则s1
如图所示,木盒中固定一质量为m的砝码,木盒和砝码在桌面上一起以初速度v0滑行一段距离s1后停止.今拿走砝码,而持续加一个竖直向下的恒力F(F=mg),其他条件不变,木盒滑行的距离s2,则s1分析:根据牛顿第二定律分别求出两种情况下的加速度,根据匀变速直线运动的速度位移公式比较位移的大小.
解答:解:设木盒的质量为M,根据牛顿第二定律得,放砝码时,加速度:a1=
=μg
拿走砝码施加F时,加速度:a2=
=μ
g
可知a2>a1.
根据v2=2ax得,x=
,知加速度增大,则滑行的距离变小.即:s1>s2
故答案为:>
| μ(M+m)g |
| m+M |
拿走砝码施加F时,加速度:a2=
| μ(Mg+F) |
| M |
| M+m |
| M |
可知a2>a1.
根据v2=2ax得,x=
| v2 |
| 2a |
故答案为:>
点评:解决本题的关键通过牛顿第二定律比较出加速度的大小,注意选择的研究对象不同,第一次选择整体,第二次选择木盒.

练习册系列答案
相关题目
 (2012?徐汇区二模)如图所示,木盒中固定一质量为m的砝码,木盒和砝码在桌面上一起以一定的初速度滑行一段距离后停止.今拿走砝码,而持续加一个竖直向下的恒力F(F=mg),其他条件不变,则木盒滑行的距离( )
(2012?徐汇区二模)如图所示,木盒中固定一质量为m的砝码,木盒和砝码在桌面上一起以一定的初速度滑行一段距离后停止.今拿走砝码,而持续加一个竖直向下的恒力F(F=mg),其他条件不变,则木盒滑行的距离( )