题目内容
钍(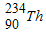 )具有放射性,能放出一个β粒子而变为镤(Pa).现有一个静止的钍(
)具有放射性,能放出一个β粒子而变为镤(Pa).现有一个静止的钍(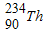 )原子核处于匀强磁场中,某时刻它放出一个β粒子,放出的β粒子的初速度与磁感应强度方向垂直.
)原子核处于匀强磁场中,某时刻它放出一个β粒子,放出的β粒子的初速度与磁感应强度方向垂直.(1)写出上述核反应方程;
(2)若
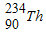 的质量为mT,β粒子的质量为me,镤(Pa)的质量为mp,真空中的光速为c,则反应中释放的核能为多少?
的质量为mT,β粒子的质量为me,镤(Pa)的质量为mp,真空中的光速为c,则反应中释放的核能为多少?(3)生成的镤(Pa)与β粒子在磁场中做匀速圆周运动的半径之比为多少?
【答案】分析:放射性元素衰变时,满足质量数和核电荷数守恒.衰变后的粒子进入磁场做匀速圆周运动,再由洛伦兹力提供向心力来求出轨道半径,并由动量守恒联立求解半径之比.
解答:解:(1)钍核衰变方程:90234Th→-1e+91234Pa
(2)根据质能方程知反应中释放的核能为E=△mC2=(mT-me-mp)C2
(3)衰变生成的粒子和新核动量守恒,根据粒子在匀强磁场中做匀速圆周运动的半径公式:r=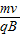 知
知
RPa:Re=qe:qPa=1:91
答:(1)核反应方程90234Th→-1e+91234Pa;
(2)反应中释放的核能为=(mT-me-mp)C2;
(3)生成的镤(Pa)与β粒子在磁场中做匀速圆周运动的半径之比为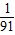 .
.
点评:带电粒子在磁场中做匀速圆周运动时,解题三步曲:定圆心、画圆弧、求半径.
解答:解:(1)钍核衰变方程:90234Th→-1e+91234Pa
(2)根据质能方程知反应中释放的核能为E=△mC2=(mT-me-mp)C2
(3)衰变生成的粒子和新核动量守恒,根据粒子在匀强磁场中做匀速圆周运动的半径公式:r=
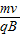 知
知RPa:Re=qe:qPa=1:91
答:(1)核反应方程90234Th→-1e+91234Pa;
(2)反应中释放的核能为=(mT-me-mp)C2;
(3)生成的镤(Pa)与β粒子在磁场中做匀速圆周运动的半径之比为
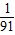 .
.点评:带电粒子在磁场中做匀速圆周运动时,解题三步曲:定圆心、画圆弧、求半径.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
钍核
Th具有放射性,它能放出一个电子衰变成镤核
Pa,伴随该过程会放出γ光子.下列说法正确的是( )
234 90 |
234 91 |
| A、原子核内部中子转变为质子时,放出电子 | ||
| B、因为衰变过程中原子核的质量数守恒,所以不会出现质量亏损 | ||
| C、若钍和其它元素反应处于化合态,钍的半衰期并不发生变化 | ||
D、γ光子是衰变过程中钍核
|

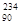 Th)具有放射性,它能放出一个电子衰变成镤核(
Th)具有放射性,它能放出一个电子衰变成镤核(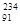 Pa),伴随该过程会放出γ光子,下列说法中正确的是_______。
Pa),伴随该过程会放出γ光子,下列说法中正确的是_______。