题目内容
16.相距为L的光滑平行导轨与水平面成θ角放置,上端连电阻R,处在与所在平面垂直的匀强磁场中,磁感应强度大小为B0,电阻为r的导体MN(质量m)垂直导轨并在两导轨上,导体MN距离上端电阻R的距离也为L.(设B0=1T,L=1m,θ=30°,m=0.1kg,R=0.8Ω,r=0.2Ω,g=10m/s2.)
(1)静止释放导体MN,求:
①MN获得的最大速度vm.
②若MN沿斜面下滑0.2m时恰好获得最大速度,求在此过程中回路一共生热多少焦?
(2)设单位时间内磁感应强度增加量为k,磁感应强度初始值为B0.现给一个平行斜面且垂直MN的外力(设沿斜面向上为外力的正方向),使导体MN始终静止在轨道上.写出外力F随时间t的变化关系式并画出F(沿斜面向上为正)随时间t的函数图象(k=1T/s).
分析 (1)导体MN由静止释放,沿导轨向下做加速运动,当导体MN所受合力为零时,导体做匀速直线运动,速度达到最大,对导体进行受力分析,由平衡条件求出导体获得的最大速度;导体克服安培力做功转化为内能,由能量守恒定律可以求出回路产生的焦耳热.
(2)由法拉第电磁感应定律求出感应电动势,由欧姆定律求出感应电流,由F=BIL求出安培力大小,由楞次定律判断出感应电流方向,由左手定值判断出安培力的方向,对导体受力分析,由平衡条件列方程求出拉力大小,然后作出图象.
解答 
安培力F安=B0IL=B0$\frac{{B}_{0}L{v}_{m}}{R+r}$L=$\frac{{B}_{0}^{2}{L}^{2}{v}_{m}}{R+r}$,
导体MN由静止开始向下做加速度减小的加速运动,当导体所受合力为零时,速度达到最大vm,由平衡条件得:
mgsin30°=F安,
则最大速度 vm=$\frac{mg(R+r)sin30°}{{B}_{0}^{2}{L}^{2}}$=0.5m/s;
②由能量守恒定律:mgxsin30°=$\frac{1}{2}$mvm2+Q,
代入数据解得:Q=0.0875J
(2)由题意知B=B0+kt,由法拉第电磁感应定律得
E′=$\frac{△Φ}{△t}$=S$\frac{△B}{△t}$=kL2
安培力:F安′=BI′L=B$\frac{E′}{R+r}$L
由平衡条件得
mgsin30°=F安′+F
联立得 F=mgsin30°-F安′=0.5-(B0+kt)$\frac{k{L}^{2}}{R+r}$L=-0.5-t(N)
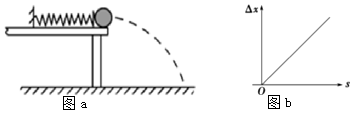
F-t图象如下图所示.
答:(1)①MN获得的最大速度vm=0.5m/s;
②若MN沿斜面下滑0.2m时恰好获得最大速度,在此过程中回路产生的热量为0.0875J.
(2)外力F随时间t的变化关系式为:F=-0.5-t(N);F-t图象如图所示.
点评 在导体MN沿轨道下滑时,导体受到的安培力是变力,当安培力达到等于重力沿斜面向下的分力时,导体导体受到的合力为零,导体做匀速直线运动,速度达到最大.

| A. | 伽利略认为自由落体运动可以认为是物体在倾角为90°的斜面上的运动,故根据铜球在斜面上的运动规律推出自由落体的运动规律,这里采用了实验和逻辑推理相结合的方法 | |
| B. | 两匹马比一匹马拉车跑得快,说明物体受力越大则速度就越大 | |
| C. | 人在沿直线加速前进的车厢内,竖直向上跳起后,将落在起跳点的后方 | |
| D. | 一个运动的物体,如果不再受力了,它总会逐渐停下来,这说明:静止状态才是物体不受力时的“自然状态” | |
| E. | 神州号飞船返回舱返回地球,打开降落伞做减速直线运动的过程,返回舱处于超重状态 |
| A. | 振幅越大,则波传播的速度越快 | |
| B. | 振幅越大,则波传播的速度越慢 | |
| C. | 在一个周期内,振动质元走过的路程等于一个波长 | |
| D. | 振动的频率越高,则波传播一个波长的距离所用的时间越短 |
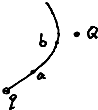 在点电荷Q形成的电场中有一个带负电的带电粒子q,其重力因远小于所受电场力而可忽略不计,它在电场中的运动轨迹如图所示,比较轨迹上a、b两点的电势和粒子通过该点时的动能,下面结论中正确的是( )
在点电荷Q形成的电场中有一个带负电的带电粒子q,其重力因远小于所受电场力而可忽略不计,它在电场中的运动轨迹如图所示,比较轨迹上a、b两点的电势和粒子通过该点时的动能,下面结论中正确的是( )| A. | Ua>Ub,Eka>Ekb | B. | Ua>Ub,Eka<Ekb | C. | Ua<Ub,Eka>Ekb | D. | Ua<Ub,Eka<Ekb |
 如图所示,L1、L2是完全相同的灯泡,L是自感系数较大、直流电阻为R0的线圈,滑动变阻器的最大阻值为R(R>R0),S由闭合到断开的瞬间,关于L1、L2亮度的说法中正确的是( )
如图所示,L1、L2是完全相同的灯泡,L是自感系数较大、直流电阻为R0的线圈,滑动变阻器的最大阻值为R(R>R0),S由闭合到断开的瞬间,关于L1、L2亮度的说法中正确的是( )| A. | 两灯都亮一下再熄灭 | B. | 两灯先后熄灭 | ||
| C. | L2灯可能亮一下再熄灭 | D. | 两灯立即熄灭 |
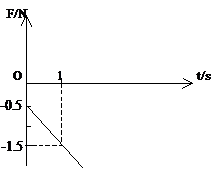
 如图所示,长方体木块A、B叠在一起,放在水平桌面上,A、B之间的接触面粗糙.B受到水平方向的拉力作用、但仍然保持静止.则A木块受到的力的个数是( )
如图所示,长方体木块A、B叠在一起,放在水平桌面上,A、B之间的接触面粗糙.B受到水平方向的拉力作用、但仍然保持静止.则A木块受到的力的个数是( )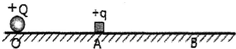 如图所示,绝缘水平地面上O点固定有电量为+Q的点电荷,一质量为m、电量为+q的可视为质点的小滑块与地面动摩擦因数为μ,从A点静止释放,最终停在B点,AB间距L,重力加速度为g,静电力常数为k,求:
如图所示,绝缘水平地面上O点固定有电量为+Q的点电荷,一质量为m、电量为+q的可视为质点的小滑块与地面动摩擦因数为μ,从A点静止释放,最终停在B点,AB间距L,重力加速度为g,静电力常数为k,求: