题目内容
9.甲、乙两个做匀速圆周运动的卫星,角速度和线速度分别为ω1、ω2和v1、v2,若它们的轨道半径之比为$\frac{r_1}{r_2}=\frac{1}{2}$,则下列表达式中正确的是( )| A. | $\frac{ω_1}{ω_2}=\frac{{2\sqrt{2}}}{1},\frac{v_1}{v_2}=\frac{1}{2}$ | B. | $\frac{ω_1}{ω_2}=\frac{{2\sqrt{2}}}{1},\frac{v_1}{v_2}=\frac{1}{{\sqrt{2}}}$ | ||
| C. | $\frac{ω_1}{ω_2}=\frac{{2\sqrt{2}}}{1},\frac{v_1}{v_2}=\frac{{\sqrt{2}}}{1}$ | D. | $\frac{ω_1}{ω_2}=\frac{{\sqrt{2}}}{1},\frac{v_1}{v_2}=\frac{1}{{\sqrt{2}}}$ |
分析 根据万有引力提供圆周运动向心力写出角速度与线速度与半径的关系,再根据半径比求得它们之比.
解答 解:根据万有引力提供圆周运动向心力有:$G\frac{mM}{{r}^{2}}=mr{ω}^{2}=m\frac{{v}^{2}}{r}$
可得$ω=\sqrt{\frac{GM}{{r}^{3}}}$,所以$\frac{{ω}_{1}}{{ω}_{2}}=\frac{\sqrt{\frac{GM}{{r}_{1}^{3}}}}{\sqrt{\frac{GM}{{r}_{2}^{3}}}}=\sqrt{(\frac{{r}_{2}}{{r}_{1}})^{3}}=\frac{2\sqrt{2}}{1}$
线速度v=$\sqrt{\frac{GM}{r}}$,所以$\frac{{v}_{1}}{{v}_{2}}=\frac{\sqrt{\frac{GM}{{r}_{1}}}}{\sqrt{\frac{GM}{{r}_{2}}}}=\sqrt{\frac{{r}_{2}}{{r}_{1}}}=\frac{\sqrt{2}}{1}$
故选:C.
点评 万有引力提供环绕天体圆周运动的向心力,能据此列式分析描述圆周运动的物理量与半径的关系是正确解题的关键.

练习册系列答案
相关题目
6. 某物体由静止开始做直线运动,物体所受合力F随时间t变化的图象如图所示,在0-8秒内,下列说法正确的是( )
某物体由静止开始做直线运动,物体所受合力F随时间t变化的图象如图所示,在0-8秒内,下列说法正确的是( )
 某物体由静止开始做直线运动,物体所受合力F随时间t变化的图象如图所示,在0-8秒内,下列说法正确的是( )
某物体由静止开始做直线运动,物体所受合力F随时间t变化的图象如图所示,在0-8秒内,下列说法正确的是( )| A. | 物体在0一2s内做匀加速直线运动 | B. | 物体在第2秒末速度最大 | ||
| C. | 物体在第8秒末离出发点最远 | D. | 物体在第4s末速度方向发生改变 |
7.关于原子核下列说法正确的是( )
| A. | 静止的原子核Ra226在匀强磁场中发生α衰变,沿着与磁场垂直的方向放出一个α粒子,此粒子的径迹与反冲核的径迹是两个相互外切的圆,α粒子轨迹半径较大 | |
| B. | 静止的原子核Th230在匀强磁场中发生β衰变,沿着与磁场垂直的方向放出一个电子,此粒子的径迹与反冲核的径迹是两个相互外切的圆,反冲核轨迹半径较大 | |
| C. | 一个U235核吸收一个中子后可能发生的反应是${\;}_{92}^{235}$U+${\;}_{0}^{1}$n→${\;}_{56}^{141}$Ba+${\;}_{36}^{92}$Kr+3${\;}_{0}^{1}$n,释放核能△E,则1kg U235反应释放能量为$\frac{1000}{235}△E$ | |
| D. | 重核裂变释放核能,生成的新核比结合能增大 |
4.某带电粒子仅在电场力作用下由A点运动到B点,运动轨迹如图所示,可以判定( )


| A. | 粒子在A点的加速度大于它在B点的加速度 | |
| B. | 粒子在A点的动能小于它在B点的动能 | |
| C. | 粒子带负电荷 | |
| D. | A点电势比B点电势低 |
14. 大量氢原子处于n=5的激发态,它们自发地跃迁到低能级,在多种可能的跃迁中,设从n=5直接跃迁到n=2和从n=5跃迁到n=1中放出光子的能量分别为E1和E2,则下面说法正确的是( )
大量氢原子处于n=5的激发态,它们自发地跃迁到低能级,在多种可能的跃迁中,设从n=5直接跃迁到n=2和从n=5跃迁到n=1中放出光子的能量分别为E1和E2,则下面说法正确的是( )
 大量氢原子处于n=5的激发态,它们自发地跃迁到低能级,在多种可能的跃迁中,设从n=5直接跃迁到n=2和从n=5跃迁到n=1中放出光子的能量分别为E1和E2,则下面说法正确的是( )
大量氢原子处于n=5的激发态,它们自发地跃迁到低能级,在多种可能的跃迁中,设从n=5直接跃迁到n=2和从n=5跃迁到n=1中放出光子的能量分别为E1和E2,则下面说法正确的是( )| A. | 从n=5跃迁可能放出8种不同频率的光子 | |
| B. | 在n=1的轨道,电子动能最小 | |
| C. | 在n=1的轨道,电子的动能和势能总和最大 | |
| D. | E1<E2 |
1. 如图所示,地面上某个空间区域存在这样的电场,水平虚线上方为场强E1,方向竖直向下的匀强电场;虚线下方为场强E2,方向竖直向上的匀强电场.一个质量m,带电+q的小球从上方电场的A点由静止释放,结果刚好到达下方电场中与A关于虚线对称的B点,则下列结论正确的是( )
如图所示,地面上某个空间区域存在这样的电场,水平虚线上方为场强E1,方向竖直向下的匀强电场;虚线下方为场强E2,方向竖直向上的匀强电场.一个质量m,带电+q的小球从上方电场的A点由静止释放,结果刚好到达下方电场中与A关于虚线对称的B点,则下列结论正确的是( )
 如图所示,地面上某个空间区域存在这样的电场,水平虚线上方为场强E1,方向竖直向下的匀强电场;虚线下方为场强E2,方向竖直向上的匀强电场.一个质量m,带电+q的小球从上方电场的A点由静止释放,结果刚好到达下方电场中与A关于虚线对称的B点,则下列结论正确的是( )
如图所示,地面上某个空间区域存在这样的电场,水平虚线上方为场强E1,方向竖直向下的匀强电场;虚线下方为场强E2,方向竖直向上的匀强电场.一个质量m,带电+q的小球从上方电场的A点由静止释放,结果刚好到达下方电场中与A关于虚线对称的B点,则下列结论正确的是( )| A. | 若AB高度差为h,则UAB=-$\frac{mgh}{q}$ | |
| B. | 带电小球在AB两点电势能相等 | |
| C. | 在虚线上下方的电场中,带电小球运动的加速度相同 | |
| D. | 两电场强度大小关系满足E2=2E1 |
18.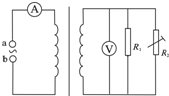 如图所示,理想变压器原、副线圈的匝数比为1:10,接线柱a、b接在电压为u=10$\sqrt{2}$sin100πtV的正弦交流电源上,R1为定值电阻,其阻值为100Ω,R2为用半导体材料制成的热敏电阻(阻值随温度升高而减小).下列说法中正确的是( )
如图所示,理想变压器原、副线圈的匝数比为1:10,接线柱a、b接在电压为u=10$\sqrt{2}$sin100πtV的正弦交流电源上,R1为定值电阻,其阻值为100Ω,R2为用半导体材料制成的热敏电阻(阻值随温度升高而减小).下列说法中正确的是( )
 如图所示,理想变压器原、副线圈的匝数比为1:10,接线柱a、b接在电压为u=10$\sqrt{2}$sin100πtV的正弦交流电源上,R1为定值电阻,其阻值为100Ω,R2为用半导体材料制成的热敏电阻(阻值随温度升高而减小).下列说法中正确的是( )
如图所示,理想变压器原、副线圈的匝数比为1:10,接线柱a、b接在电压为u=10$\sqrt{2}$sin100πtV的正弦交流电源上,R1为定值电阻,其阻值为100Ω,R2为用半导体材料制成的热敏电阻(阻值随温度升高而减小).下列说法中正确的是( )| A. | t=$\frac{1}{600}$ s时,a、b两点间电压的瞬时值为5$\sqrt{2}$V | |
| B. | t=$\frac{1}{600}$ s时,电压表的读数为50$\sqrt{2}$V | |
| C. | 在1分钟内电阻R1上产生的热量为6000J | |
| D. | 当R2的温度升高时,电压表示数变大,电流表示数变大 |
19.在用滴水法测定重力加速度的实验中,调整自来水管的阀门(开关),使得第一滴水落地时,第二滴水正好开始下落,测出从第一滴水开始下落到第N滴水落地所用的时间为t,以及水下落的高度为h,滴水的周期为T.则所测重力加速度g 及T的表达式应为( )
| A. | g=$\frac{2h{N}^{2}}{{t}^{2}}$ | B. | g=$\frac{h{N}^{2}}{{t}^{2}}$ | C. | g=$\frac{2h(N-1)^{2}}{{t}^{2}}$ | D. | g=$\frac{2h(N+1)^{2}}{{t}^{2}}$ |
 如图所示,水平面上有一重为40N的物体,受到向左F1=12N和向右F2=6N的水平力作用而保持静止.已知物体与水平面间的动摩擦因数μ=0.2,求:
如图所示,水平面上有一重为40N的物体,受到向左F1=12N和向右F2=6N的水平力作用而保持静止.已知物体与水平面间的动摩擦因数μ=0.2,求: