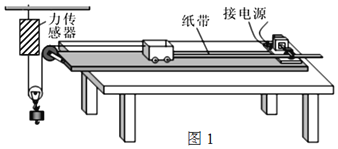
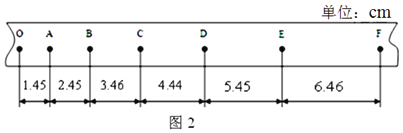
题目内容
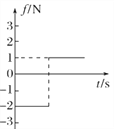
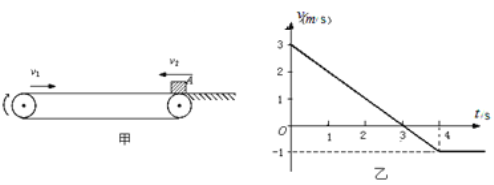
【题目】如图甲所示,绷紧的水平传送带始终以恒定速率v1运行,一质量m=1kg,初速度大小为v2的煤块从与传送带等高的光滑水平地面上的A处滑上传送带.若以地面为参考系,从煤块滑上传送带开始计时,煤块在传送带上运动的速度-时间图象如图乙所示,取g=10m/s2,求:
(1)煤块与传送带间的动摩擦因数;
(2)煤块在传送带上运动的时间;
【答案】(1)0.1 (2)8s
【解析】
(1)由v-t图,求出煤块做匀变速运动的加速度,由牛顿第二定律求出动摩擦因数;(2)由图知,最后匀速运动时和传送带速度相等,读出煤块的初速度和传送带的速度,由位移公式分别求出三段位移,把三个时间相加得在传送带上运动的时间;
(1)由速度-时间图象,煤块匀变速运动的加速度:![]() ,
,
由牛顿第二定律得:μmg=ma,
煤块与传送带间的动摩擦因数:![]()
(2)由速度-时间图象,传送带速度大小:v1=1m/s,煤块初速度大小v2=3m/s,
煤块在传送带上滑动:t1=4s与传送带相对静止.
前3s内煤块的位移:![]() ,方向向左,
,方向向左,
后1s内煤块的位移:![]() ,方向向右,
,方向向右,
4s内煤块的位移:s=s1-s2=4m,方向向左,
煤块接着在传送带上向右匀速运动,时间:![]()
故煤块在传送带上运动的时间t=t1+t2=8s.

练习册系列答案
相关题目